x=4
Объяснение:
в изображении ..........
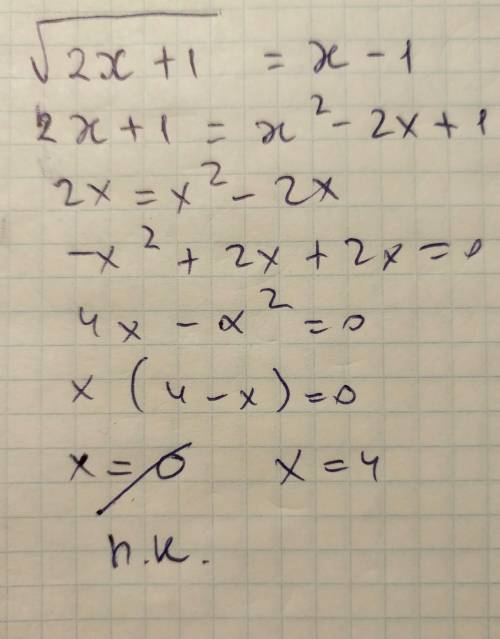
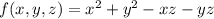
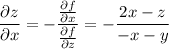
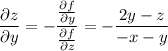
с координатами 
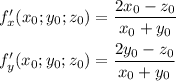
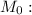
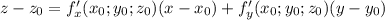- уравнение касательной в общем виде.
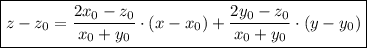- уравнение касательной плоскости к поверхности в точке с координатами 
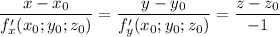
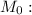
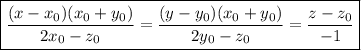- каноническое уравнение нормали к поверхности в точке с координатами
4
Объяснение:
возведем в квадрат ;
2x+1=x²-2x+1
2x+1-x²+2x-1=0
-x²+4x=0
x²-4x=0
x(x-4)=0
x=0 ; 4
0 не подходит по одз!