6) 2ab - 2ac + 3b - 3c = 2ab + 3b - 2ac - 3c = b(2a+3) - c(2a+3) = (b-c)(2a+3)
7) 5ax + 10ay + bx + 2by = x(5a+b) + 2y(5a+b)= (5a+b)(2y+x)
8) 3ac + 6bc + 7ax +14bx= 3c(a+2b) + 7x(a+2b) = (3c+7x)(a+2b)
9) 2ax + 2xy - an - yn = 2x(a+y) - n(a+y) = (2x-n)(a+y)
10) 
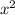+ xz + ax + az = x(x+z) + a(x+z) = (x+a)(x+z)
11) ax + 3ay + 5x + 15y= a(x+3y) + 5(x+3y) = (x+3y)(a+5)
12) 2bc + ac + 6b + 3a = c(2b+a) + 3(2b+a) = (2b+a)(3+a)
13) xy - 
- ax + ay= x(y-a) - a(y-a) = (y-a)(x-a)
14) ab - ac - + bc = a(b-a) - c(b-a)= (b-a)(a-c)
15) 
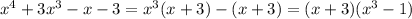далее разложение, если знаешь формулу разности кубов ---------------------------------
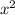(x+3)(x-1)(+x+1)
√3 ·sin(2πcosx)+cos(2πcosx)=1 |:2
(√3)/2 ·sin(2πcosx)+(1/2)cos(2πcosx)=1/2
Вспомним, что сos(π/6)=(√3)/2, а sin(π/6)=1/2. Тогда можно переписать равенство:
sin(2πcosx)·сos(π/6)+cos(2πcosx)·sin(π/6)=1/2
По формуле синуса суммы, получим:
sin(2πcosx+(π/6))=1/2
Откуда
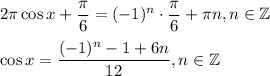
|cosx|≤1, поэтому подходят только n={-2;-1;0;1;2}
Соответственно cosx = {-1;-2/3;0;2/3;1}
Решая простейшие тригонометрические уравнения НА ТРИГОНОМЕТРИЧЕСКОМ КРУГЕ, запишем красивый ответ для x.
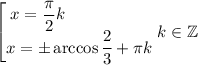
Формально стоил ввести 5 переменных для каждого значения cosx т.к. все значения не зависит друг от друга. Но тогда ответ был бы громоздким. К тому же если рассматривать всё множество действительных чисел, то я указал все решения уравнения.
ответ: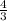
Объяснение:
Площадь данной фигуры находится при определенного интеграла. Известны его границы из условия x = 1; 2
Мы получили первообразную функции. Подставляем в нее значения x: