 -4
-4 +4 м. Найти скорость и ускорение при t+1c.
+4 м. Найти скорость и ускорение при t+1c. ×㏑x)°
×㏑x)°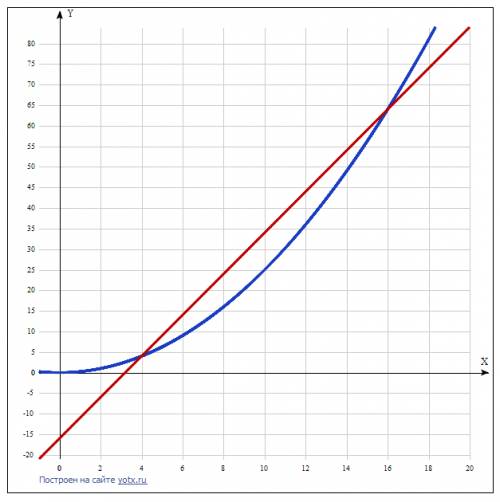
 . Графиком данной функции является парабола, ветви которой направлены вверх. Следовательно, минимальное значение функции соответствует вершине параболы.
. Графиком данной функции является парабола, ветви которой направлены вверх. Следовательно, минимальное значение функции соответствует вершине параболы.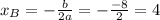
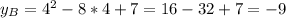
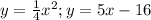
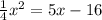
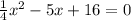
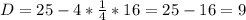
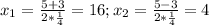
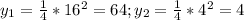
1) v=s'(t)=9*t²-8*t м/с, a=v'(t)=18*t-8 м/с².
2) [x²*ln(x)]'=2*x*ln(x)+x.
Объяснение:
1) скорость v=s'(t)=9*t²-8*t м/с, ускорение a=v'(t)=18*t-8 м/с².
2) [x²*ln(x)]'=2*x*ln(x)+x²*1/x=2*x*ln(x)+x.