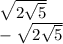
a + b = -8
Объяснение:
1 уравнение
x^3 - 4x^2 - x - a = 0
2 уравнение
x^2 - x - b = 0
Если они имеют 2 общих корня, то 2 уравнение имеет 2 корня.
D = 1^2 - 4(-b) = 4b + 1
x1 = (1 - √(4b+1))/2
x2 = (1 + √(4b+1))/2
И оба этих корня должны подходить к 1 уравнению.
Подставляем x1 и x2, получаем систему
{ (1 - √(4b+1))^3/8 - 4*(1 - √(4b+1))^2/4 - (1 - √(4b+1))/2 - a = 0
{ (1 + √(4b+1))^3/8 - 4*(1 + √(4b+1))^2/4 - (1 + √(4b+1))/2 - a = 0
Раскрываем скобки
{ (1-3√(4b+1)+3(4b+1)-(4b+1)√(4b+1))/8-(1-2√(4b+1)+(4b+1))-1/2+√(4b+1)/2-a=0
{ (1+3√(4b+1)+3(4b+1)+(4b+1)√(4b+1))/8-(1+2√(4b+1)+(4b+1))-1/2-√(4b+1)/2-a=0
После нескольких тождественных преобразований получаем:
{ -5b/2 - 2 - b√(4b+1)/2 + 2√(4b+1) - a = 0
{ -5b/2 - 2 + b√(4b+1)/2 - 2√(4b+1) - a = 0
Складываем уравнения
-5b/2 - 2 - b√(4b+1)/2 + 2√(4b+1) - a - 5b/2 - 2 + b√(4b+1)/2 - 2√(4b+1) - a = 0
-5b - 4 - 2a = 0
a = -5b/2 - 2
Подставляем в любое уравнение
-5b/2 - 2 - b√(4b+1)/2 + 2√(4b+1) + 5b/2 + 2 = 0
- b√(4b+1)/2 + 2√(4b+1) = 0
b = 4
a = -5*4/2 - 2 = -10 - 2 = -12
Сумма a + b = 4 - 12 = -8
1) 5 подарочных наборов и 5 коробок
как можно разместить?
В первую коробку мы можем положить любой из 5 наборов
во вторую коробку - любой из 4
в третью- любой из 3
в 4ю- любой из 2
и в 5-ю оставшийся набор
всего
2) даны цифры 1,2,3,4,7
нужно составить 4-х значное число- кратное 6
На 6 делятся числа кратные 2 и 3
кратные 2 должны оканчиваться на 2 или 4
кратные трем должны давать в семме цифр числа - число кратное 3
Первый вариант- наше число заканчивается на 2
тогда на оставшиеся 3 места идут 1,3,4,7
но 1+3+4+2 не кратно 3, 1+3+7+2 не кратно 3, 1+4+7+2 не кратно 3 и 3+4+7+2 не кратно 3
Второй вариант- наше число заканчивается на 4
тогда единственная комбинация это число состоящее из цифр 1,3,7, и 4
Количество таких чисел 3*2*1=6
3) Есть 6 маек и 4 наклейки
первую наклейку клеим на любую из 6, вторую на любую из 5, третью- на любую из 4 и последнюю наклейку на любую из 3
тогда всего
Объяснение:
Нужно написать:
Уравнение имеет вид:
Уравнение составлено!