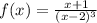Пусть х км/ч - это скорость, с которой ехал велосипедист из пункта А в пункт В
Так как длина путь из пункта А в пункт В = 27 километров.Тогда путь из пункста А в пункт В он проехал за 27/х(часов) - потому что на обратном пути велосипедист уменьшил скорость на 3км/ч, следовательно:х-3км/ч - скорость велосипедиста.(потому что обратный путь был короче на 7 километров), то есть он равен: 27-7=20(км), следовательно:20/(х-3) часов - это он потратил на обратный путь.А по условию на обратный путь он затратил всего 10минут, а это 1/6 часа меньше.
Составим уравнение:
27/х-1/6=20/(х-3)
Надо обе части умножить на 6х*(х-3) не равное нулю, тоесть х≠0 и х≠3(ЭТО НАМ НЕ ПОДХОДИТ)=>
162*(х-3)-х*(х-3)=120х
162х-486-х2+3х-120=0
Теперь на всё это умножить на (-1) и привести конечно-же подобные слогаемые.
х2-45х+486=0
Всё получим мы через теорему Виета:
х1+х2=45
х1*х2=486
х1=18
х2=27
Либо через Дискриминант, то будет так.
Дискриминант=(-45)2-4*2*486=2025+1944=3969
х1,2=54(плюс/минус)63/4
х1 = 18
х2 = 27
ответ: 18км/ч, 27км/ч.
, если f(1)=1, подробнее если можно
(3+y)² - 4 = (3+у)²-2² = (3+у-2)(3+у+2) = (у+1)(у+5)
(3x+1)² - (4x-3)² = (3х+1-4х+3)(3х+1+4х-3) = (-х+4)(7х-2)
100 - 49x²y² = 10²-(7ху)² = (10-7ху)(10+7ху)
(5+x)² - 9 = (5+х)²-3² = (5+х-3)(5+х+3) = (х+2)(х+8)
(2a + 7)² - (3a - 5)² = (2а+7-3а+5)(2а+7+3а-5) = (-а+12)(5а+2)
2. x²ⁿ - 9 = (хⁿ)²-3² = (хⁿ-3)(хⁿ+3)
b² - a⁴ⁿ = b² - (a²ⁿ)² = (b-a²ⁿ)(b+a²ⁿ)
x²ⁿ - y²ⁿ = (хⁿ)²-(уⁿ)² = (хⁿ-уⁿ)(хⁿ+уⁿ)
81a⁸ⁿ - 16 = (9а⁴ⁿ)²-4² = (9а⁴ⁿ-4)(9а⁴ⁿ+4) = (3а²ⁿ-2)(3а²ⁿ+2)(9а⁴ⁿ+4)
a²ⁿ - 1 = (аⁿ)²-1² = (аⁿ-1)(аⁿ+1)
x²- y⁴ⁿ = х²-(у²ⁿ)² = (х-у²ⁿ)(х+у²ⁿ)
a⁴ⁿ - b⁴ⁿ = (а²ⁿ)²-(b²ⁿ)² = (a²ⁿ-b²ⁿ)(a²ⁿ+b²ⁿ) = (aⁿ-bⁿ)(aⁿ-bⁿ)(a²ⁿ+b²ⁿ)
49x^6m - 25 = (7x^3m)² - 5² = (7x^3m - 5)(7x^3m + 5)