Если речь идёт о преобразовании выражений, то все арифметические действия сохраняются и выполняются после знака равенства.
Если речь идёт о решении уравнений, то перенести арифметическое действие через знак равенства невозможно. Можно перенести через знак равенства множители, и с другой стороны они станут делителями. Можно перенести через знак равенства делители, и с другой стороны они станут множителями.
Например, множители a и b слева становятся делителями справа
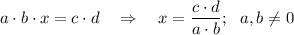
Например, делители a и b слева становятся множителями справа
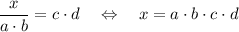
Такие действия возможны вследствие тождественных преобразований верных равенств.
Если обе части верного равенства умножить на одно и то же число, равенство останется верным :
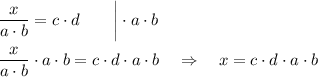
Если обе части верного равенства разделить на одно и то же не равное нулю число, то равенство останется верным :
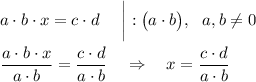

y=x^2+18x+77
y=2x+22
построю графики и найду точки пересечения их
x^2+18x+77=2x+22
x^2+16x+55=0
D=256-220=36
x1=(-16+6)/2=-5; x2=(-16-6)/2=-11
для построения прямой достаточно 2 точки
(-11;0);(-2;12)
для построения параболы найду ее вершину
x=-b/(2a)=-18/2=-9
y(-9)=81-162+77=-4
y(-11)=121-198+77=0
y(-5)=25-90+77=12
S=∫(2x+22-(x^2+18x+77)dx=∫(-x^2-16x-55)dx=-x^3/3-16x^2/2-55x=
=-(x^3/3+8x^2+55x)=
подстановка по х от -11 до -5
=-(-125/3+200-275-(-1331/3+968-275))=116 2/3-80 2/3=36