Question

с заданием! Вычислить несобственные интегралы или установить их расходимость:

Answer 1

$2\pi - 1$

Объяснение:

Подыинтегральная функция на указанном промежутке интегрирования имеет единственную особенность в точке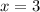 $x=3$. Исследовать интеграл на сходимость в этой точке можно с признака сравнения. В окрестности данной точки данный интеграл эквивалентен интегралу:

$\int\limits_{3}^{4} \frac{dx}{\sqrt{x-3}} = 2\sqrt{x-3}|^{4}_{3} = 2,$

то есть исходный интеграл сходится на заданном промежутке. Найдем его:

$\int\limits_{3}^{4} \frac{x}{\sqrt{(x-3)(5-x)}}\,dx = \int\limits_{3}^{4} \frac{x}{\sqrt{-x^2+8x-15}}\,dx = -\frac{1}{2}\int\limits_{3}^{4} \frac{-2x+8-8}{\sqrt{-x^2+8x-15}}\,dx = -\frac{1}{2}\int\limits_{3}^{4} \frac{-2x+8}{\sqrt{-x^2+8x-15}}\,dx + \frac{1}{2}\int\limits_{3}^{4} \frac{8}{\sqrt{-x^2+8x-15}}\,dx = -\frac{1}{2}\int\limits_{3}^{4} \frac{d(-x^2+8x-15)}{\sqrt{-x^2+8x-15}}\,dx+ 4\int\limits_{3}^{4} \frac{d(x-4)}{\sqrt{1-(x-4)^2}} = -\sqrt{-x^2+8x-15}|^{4}_{3} + 4arcsin(x-4)|^{4}_{3} = -1+2\pi$