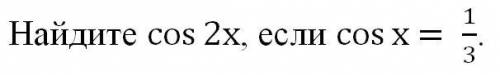
Пересечение двух прямых даёт 4 угла. Сумма трёх равна 228°. Сумма 4 углов должна быть равна 360°.
Найдём 4 угол:
360 - 228 = 132° → Вертикальный угол 4-му углу тоже равен 132° по свойству вертикальных углов.
Получается уже известны 2 угла ( каждый по 132° ), а их сумма равна:
132 + 132 = 264°
Найдём сумму оставшихся 2-ух углов:
360 - 264 = 96°
Так как мы узнали еще два вертикальных угла, то по свойству вертикальных углов, они равны между собой, поэтому сумму этих 2-ух углов мы делим пополам:
96 / 2 = 48°
ответ: 132°, 48°, 132°, 48° (если идти по часовой стрелке)
1.
а) a + 3 < 2a,
а - 2а < -3,
-a < -3,
a > 3
a ∈ (3; +∞)
б) 5 - b < 6b + 4,
-b - 6b < 4 - 5,
-7b < -1,
b > 1/7
b ∈ (1/7; +∞)
2. x² - 4x - 5 ≤ 0
Рассмотрим функцию у = x² - 4x - 5. Графиком данной функции является параола, ветви которой направлены вверх. Выясним, где функция принимает незначения, меньшие или равные 0.
Найдем нули функции у = x² - 4x - 5.
x² - 4x - 5 = 0
D = (-4)² - 4 · 1 · (-5) = 16 + 20 = 36; √36 = 6
x₁ = (4 + 6))(2 · 1) = 10/2 = 5
x₂ = (4 - 6))(2 · 1) = -2/2 = -1
+ - +
||
-1 5
x ∈ [-1; 5]
ответ: [-1; 5].
-7/9
Объяснение:
cos x=1/3
cos (2x) =?
По теореме Пифагора: =
√3²-1²=√(3-1)(3+1)=√2*4=√8=2√2
Найдем косинус.
2cos²(x)-1=cos2x=2*(1/3)²-1=2*(1/9)-1=(2/9)-1= -7/9