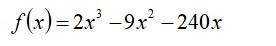
ответ:f(x) возрастает на (-∞;-5) ∪ (8;+∞), f(x) убывает на (-5;8)
Объяснение:1)найдём ОДЗ: х∈R;
2) f'(x)= 6x²-18x-240
3) найдём критические точки, для чего приравняем производную к нулю: f'(x)=0, если 6x²-18x-240=0 ⇒x²-3x-40=0 ⇒ дискриминант D= 9+160=169=13² ⇒ x₁=(3+13)/2=8, x₂=(3-13)/2= -5, т.е. x₁=8, x₂= -5 - критические точки
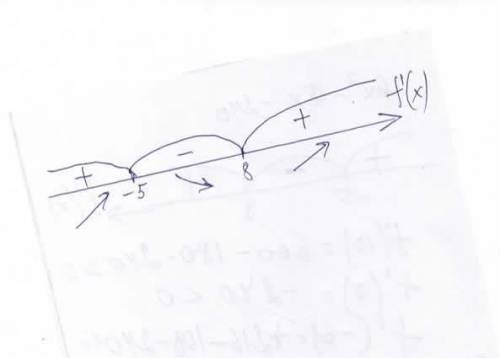
4) Отметим критические точки на координатной прямой, они разбивают её на 3 интервала (выполнить рисунок): (-∞;-5), (-5;8), (8;+∞). Найдём знак производной в каждом из этих интервалов:
на (-∞;-5) f'(x)>0;
на (-5;8) f'(x)<0;
на (8;+∞) f(x)>0
если производная функции y=f(x) положительна для любого x из интервала (a;b), то функция возрастает на (a;b);
если производная функции y=f(x) отрицательна для любого x из интервала (a;b) , то функция убывает на (a;b) .
Значит f(x) возрастает на (-∞;-5) ∪ (8;+∞), f(x) убывает на (-5;8)
1) 3х - 7 < x + 1,
3x - x < 1 + 7,
2x < 8,
x < 4.
ответ: х ∈ (-∞; 4).
2) 2 + x > 8 - x,
x + x > 8 - 2,
2x > 6,
x > 3.
ответ: х ∈ (3; +∞).
3) 1 - x ≥ 2x - 5,
-x - 2x ≥ -5 - 1,
-3x ≥ -6,
x ≤ 2.
ответ: х ∈ (-∞; 2].
4) 2x + 1 > x + 6,
2x - x > 6 - 1,
x > 5.
ответ: х ∈ (5; +∞).
5) 4x + 2 > 3x + 1,
4x - 3x > 1 - 2,
x > -1.
ответ: х ∈ (-1; +∞).
6) 6x + 1 < 2x + 9,
6x - 2x < 9 - 1,
4x < 8,
x < 2.
ответ: х ∈ (-∞; 2).
h(t) = 30t − 6t²
Даже ничего не зная, можно в уме подставить значения t, в эту функцию...
h(0) = 30 • 0 − 6 • 0 = 0 — вначале высота нулевая
h(1) = 30 • 1 − 6 • 1 = 24 — через 1 секунду. высота = 24 метров
h(2) = 30 • 2 − 6 • 4 = 36 — через 2 секунды будет 36 метров
h(3) = 30 • 3 − 6 • 9 = 36 — оппа. Значит где-то между 2-й и 3-й секундой мячик дошел до максимальной высоты и начал снова падать.
h(4) = 30 • 4 − 6 • 16 = 24
h(5) = 30•5 − 6•25 = 0 — оппа. Ничего не зная можно было выяснить, что мяч упадет на землю через 5 секунд!)
А максимум функции можно найти, если решить уравнение "производная функции" = 0
h'(t)= 30 - 12t
30 - 12t = 0
12t = 30
t = 5 / 2 = 2.5
Т. е. максимума достигает через 2.5 секунды.
h(2.5)= 30 • 2.5 - 6 • 6.25 = 37.5
Максимальная высота: 37.5 метров;
Упадет на землю спустя 5 секунд после удара
производная равна 6х²-18х-240
Найдем критические точки.
6х²-18х-240=0
х²-3х-40=0
По Виету х=8; х=-5
установим знаки производной на области определения функции
-58
+ - +
промежуток убывания [-5;8]