1) Находим производную f'(x)=6*x²-6. 2) Приравнивая её нулю, получаем уравнение 6*(x²-1)=0, решая которое, находим x1=1 и x2=-1. 3) Пусть x<-1, тогда f'(x)>0. Пусть -1<x<1, тогда f'(x)<0. Пусть x>1, тогда f'(x)>0. Так как при переходе через точку x=-1 производная меняет знак с + на -, то эта точка является точкой максимума. Так как при переходе через точку x=1 производная меняет знак с - на +, то эта точка является точкой минимума. Однако по условию нас интересует лишь интервал [0;2], а на нём есть лишь одна точка экстремума - точка минимума x=-1. Тогда минимальное значение функции на этом интервале Ymin=f(1)=-3. На интервале [0;1] функция непрерывно убывает, поэтому наибольшее значение на этом интервале она принимает в его левом конце: Ymax1=f(0)=1. На интервале [1;2] функция непрерывно возрастает, поэтому наибольшее значение на этом интервале она принимает в его правом конце: Ymax2=f(2)=5. Так как Ymax2>Ymax1, то наибольшее значение функции на интервале [0;2] Ymax=Ymax2=5. ответ: Ymin=-3, Ymax=5.
⇒ cos∝ будет положительным
и ∈ (1,5
; 2
Так как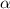
∈ 1,5π;2π , то 
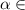4 четверти, косинус 4й четверти +