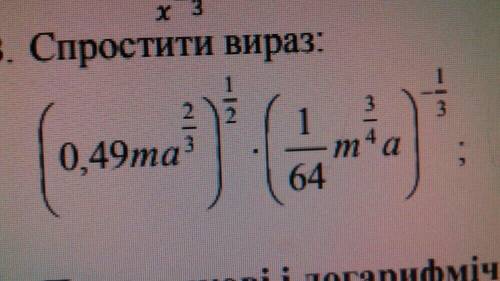
![(0,49ma^{\frac{2}{3}})^{\frac{1}{2}}*(\frac{1}{64}m^{\frac{3}{4}}a)^{-\frac{1}{3}}=[(\frac{7}{10})^{2}]^{\frac{1}{2}}*m^{\frac{1}{2}}*[(a^{\frac{2}{3}})]^{\frac{1}{2}}*[(\frac{1}{4})^{3}]^{-\frac{1}{3}}*[(m^{\frac{3}{4}})]^{-\frac{1}{3}}*a^{-\frac{1}{3}} =\\=0,7m^{\frac{1}{2}}a^{\frac{1}{3}}*4m^{-\frac{1}{4}}a^{-\frac{1}{3}}=2,8m^{\frac{1}{2}-\frac{1}{4}}a^{\frac{1}{3}-\frac{1}{3}}=2,8m^{\frac{1}{4}}a^{0}=2,8m^{\frac{1}{4}} \\\\Otvet:\boxed{2,8m^{\frac{1}{4}}}](/tpl/images/1354/2458/8a027.png)
Решение на фото/////

№1
Треугольник со сторонами 3, 4, 5 называют египетским треугольником.
№2
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
№3
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
№4
прямоугольник, у которого все стороны равны
№5
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
№6
произведению смежных сторон
№7
S=ah
№8
отрезок, соединяющий середины двух его сторон треугольника
№9
Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
№10
1/2
