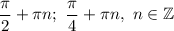Question

Решить уравнение: sin2x=√2|cosx|

Answer 1

$\sin2x=\sqrt{2} |\cos x|$

1. Раскроем модуль при условии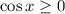 $\cos x\geq 0$:

$\sin2x=\sqrt{2} \cdot\cos x$

$2\sin x\cos x-\sqrt{2} \cdot\cos x=0$

$\cos x(2\sin x-\sqrt{2}) =0$

$\left[\begin{array}{l} \cos x=0\\ 2\sin x-\sqrt{2} =0\end{array}$

$\left[\begin{array}{l} \cos x=0\\ \sin x=\dfrac{\sqrt{2} }{2}\end{array}$

$\left[\begin{array}{l} x=\dfrac{\pi}{2}+\pi n \\ \left[\begin{array}{l} x=\dfrac{\pi }{4}+2\pi n \\ x=\dfrac{3\pi }{4}+2\pi n \end{array}\end{array},\ n\in\mathbb{Z}$

Однако корни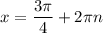 $x=\dfrac{3\pi }{4}+2\pi n$ не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ:

$\left[\begin{array}{l} x=\dfrac{\pi}{2}+\pi n \\x=\dfrac{\pi }{4}+2\pi n \end{array},\ n\in\mathbb{Z}$

2. Раскроем модуль при условии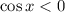 $\cos x$:

$\sin2x=-\sqrt{2} \cdot\cos x$

$2\sin x\cos x+\sqrt{2} \cdot\cos x=0$

$\cos x(2\sin x+\sqrt{2} )=0$

$\left[\begin{array}{l} \cos x=0\\ 2\sin x+\sqrt{2} =0\end{array}$

Заметим, что первое уравнение не удовлетворят условию раскрытия модуля. Продолжаем решать только второе уравнение:

$\sin x=-\dfrac{\sqrt{2} }{2}$

$\left[\begin{array}{l} x=-\dfrac{\pi }{4}+2\pi n \\ x=-\dfrac{3\pi }{4}+2\pi n \end{array},\ n\in\mathbb{Z}$

Однако корни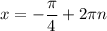 $x=-\dfrac{\pi }{4}+2\pi n$ не удовлетворяют условию раскрытия модуля. Поэтому окончательный ответ этого случая:

$x=-\dfrac{3\pi }{4}+2\pi n$

3. Объединим решения, полученные в предыдущих пунктах:

$\left[\begin{array}{l} x=\dfrac{\pi}{2}+\pi n \\x=\dfrac{\pi }{4}+2\pi n\\ x=-\dfrac{3\pi }{4}+2\pi n \end{array},\ n\in\mathbb{Z}$

Или более кратко:

$\left[\begin{array}{l} x=\dfrac{\pi}{2}+\pi n \\x=\dfrac{\pi }{4}+\pi n \end{array},\ n\in\mathbb{Z}$

ответ: $\dfrac{\pi}{2}+\pi n;\ \dfrac{\pi }{4}+\pi n,\ n\in\mathbb{Z}$