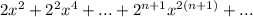
1) x ∈ (-∞; -8) U (3; +∞)
2) x ∈ (-∞; -3) U (5; 7)
Объяснение:
1) x^2 + 5x - 24>0
x^2 + 5x - 24=0
D= √(b^2 - 4ac) = √(5^2 - 4 * 1 * (-24)) = √(25 + 96) = √121 = 11
x = (-b +/- √D)/2a
x1 = -5 + 11 / 2 =3
x2 = -5-11 /2 = -8
Получается три интервала:
x<-8
-8<x<3
x>3
чередуем знаки справа налево, первый - плюс (так как нам нужно больше, то выбираем там, где плюс)
получаем x<-8 и x>3
2) (x-5)(x-7)(x+3)<0
(x-5)(x-7)(x+3)=0
x = 0 тогда, когда один из множителей равен нулю:
x=5; x=7; x=-3
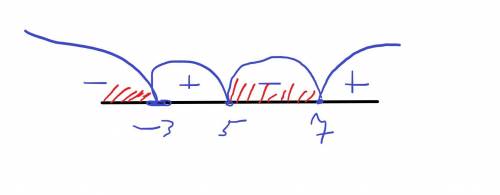
получаем четыре интервала (см фотку)
выбераем там, где минус, т. к. нужен знак < по условию
x<-3 и 5<x<7
В первом задании используешь теорему, что при (x²)³ = х⁶(степени умножаются), а при x²×x³ = x⁵(степени складываются). Дальше подставляешь икс и решено.
Во втором задании v36 = 6. Используй теорему, что vx×vy = v(x×y), где v - знак корня.
В 3.1 задании используй теорему Виета, которая гласит, что сумма двух корней равна -b, а их произведение с(в твоём случае 7). Тебе нужна сумма, поэтому просто запишешь число -b. Не забывай, что если вместо b у тебя отрицательное число(как у тебя), то всё работает так: -(-5)=5.
В 3.2 задании 2х²-3х²-2х = -х²-2х = 0.
Из этого просто -х выводишь за скобки и выполняешь уравнение.
В 4 задании вам нужно сперва найти катет АС, для этого нужна теорема Пифагора: АС²=АВ²-ВС². Находишь АС² и из этого берёшь корень.
Теперь используй теорему, что средняя линия треугольника равна половине стороны, которой параллельна. То есть, MN=½AC. Задача решена!
В 5 задании могу лишь сказать, что диагонали квадрата являются биссектрисами угла. Если у трапеции два угла равны, то она может быть равнобедренной или прямоугольной. Если в треугольнике один из углов равен 30°, то противоположная сторона равна половине гипотенузы.
Имеем степенной ряд. Здесь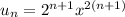 и
и 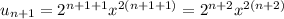
Для ряда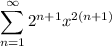 составим ряд из абсолютных величин:
составим ряд из абсолютных величин:
Пусть ряд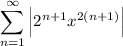 сходится при заданном значении
сходится при заданном значении  . Тогда этот ряд является знакоположительным и по признаку Даламбера:
. Тогда этот ряд является знакоположительным и по признаку Даламбера:
Тогда ряд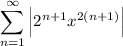 сходится на интервале
сходится на интервале 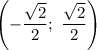
Радиус сходимости: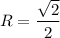
Исследуем на сходимость ряд на концах интервала.
1) Если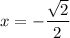 , то
, то 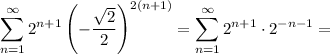
Ряд сходится. Точка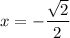 входит в область сходимости ряда.
входит в область сходимости ряда.
2) Если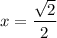 , то
, то 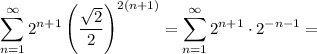
Ряд сходится. Точка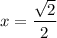 входит в область сходимости ряда.
входит в область сходимости ряда.
ответ:![\left[-\dfrac{\sqrt{2}}{2} ; \ \dfrac{\sqrt{2}}{2} \right]](/tpl/images/1356/4255/41e14.png)