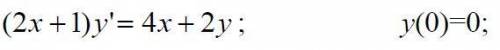
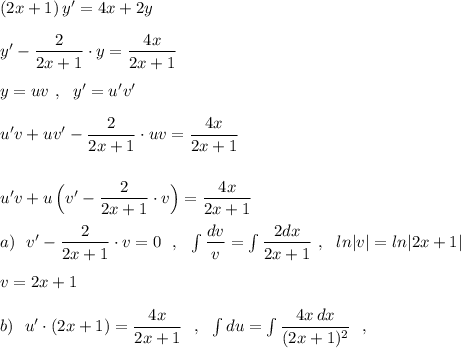
![\int \dfrac{4x\, dx}{(2x+1)^2}=\Big[\ t=2x+1\ ,\ x=\dfarc{t-1}{2}\ ,\ dx=\dfrac{dt}{2}\ \Big]=\\\\=\int \dfrac{(2t-2)\cdot \frac{1}{2}\, dt}{t^2}=\int \dfrac{t-1}{t^2}\, dt=\int \Big(\dfrac{1}{t}-\dfrac{1}{t^2}\Big)\, dt=\\\\=ln|t|+\dfrac{1}{t}+C=ln|2x+1|+\dfrac{1}{2x+1}+C\ ;\\\\u=ln|2x+1|+\dfrac{1}{2x+1}+C\\\\c)\ \ y=uv=(2x+1)\Big(ln|2x+1|+\dfrac{1}{2x+1}+C\Big)\\\\d)\ \ y(0)=0:\ \ y(0)=1\cdot (ln1+1+C)=0\ ,\ C=-1\\\\y_{chastn.}=(2x+1)\cdot \Big(ln|2x+1|+\dfrac{1}{2x+1}-1\Big)](/tpl/images/1356/9931/1e619.png)
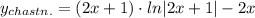
№412.
Пусть имеется х кг апельсинов. В пакет вмещается х/3 кг, в коробку - х/5 или х/3-2 кг. Составим и решим уравнение:
х/5=х/3-2 |*15
3x=5х-30
5х-3х=30
2х=30
х=30:2
х=15
ответ: имеется 15 килограммов апельсинов.
№413(б).
Пусть n - первое нечётное число, тогда два последующих нечётных числа - (n+2) и (n+4). Их сумма равна n+n+2+n+4 или 69. Составим и решим уравнение:
n+n+2+n+4=69
3n=69-6
3n=63
n=63:3
n=21
n+2=21+2=23
n+4=21+4=25
ответ: да, это числа 21, 23 и 25.
№414(б).
Пусть купили х линеек, тогда кистей купили (х+7), а карандашей - 4х. Всего купили х+х+7+4х или 43 предмета. Составим и решим уравнение:
х+х+7+4х=43
6х=43-7
6х=36
х=36:6
х=6
х+7=6+7=13
4х=4*6=24
ответ: купили 6 линеек, 13 кистей и 24 карандаша.
№412.
Пусть имеется х кг апельсинов. В пакет вмещается х/3 кг, в коробку - х/5 или х/3-2 кг. Составим и решим уравнение:
х/5=х/3-2 |*15
3x=5х-30
5х-3х=30
2х=30
х=30:2
х=15
ответ: имеется 15 килограммов апельсинов.
№413(б).
Пусть n - первое нечётное число, тогда два последующих нечётных числа - (n+2) и (n+4). Их сумма равна n+n+2+n+4 или 69. Составим и решим уравнение:
n+n+2+n+4=69
3n=69-6
3n=63
n=63:3
n=21
n+2=21+2=23
n+4=21+4=25
ответ: да, это числа 21, 23 и 25.
№414(б).
Пусть купили х линеек, тогда кистей купили (х+7), а карандашей - 4х. Всего купили х+х+7+4х или 43 предмета. Составим и решим уравнение:
х+х+7+4х=43
6х=43-7
6х=36
х=36:6
х=6
х+7=6+7=13
4х=4*6=24
ответ: купили 6 линеек, 13 кистей и 24 карандаша.