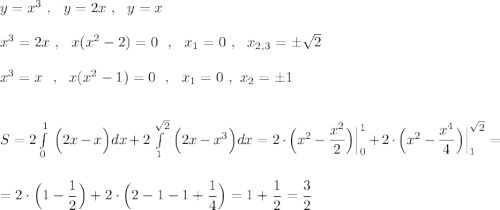
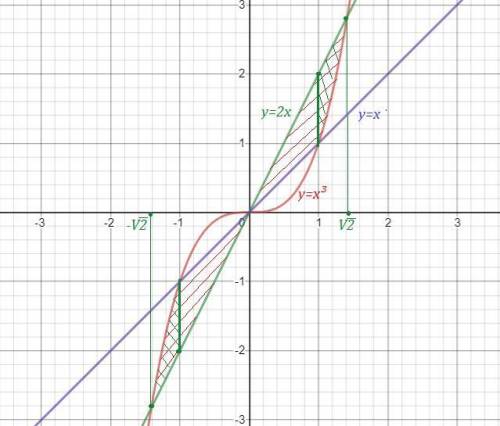
Объяснение: смотрите график и решение во вложении

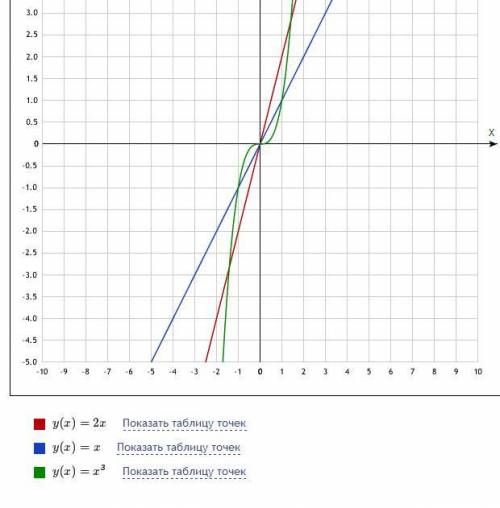
Объяснение:
1. a₁=-2 a₁₀=16 a₁₂=?
a₁₀=a₁+(10-1)*d=16
-2+9*d=16
9*d=18 |÷9
d=2 ⇒
a₁₂=a₁+(12-1)*d=-2+11*2=-2+22=20
ответ: а₁₂=20.
2. a₇=43 a₁₅=3 a₁₂=?
{a₇=a₁+6d=43
{a₁₅=a₁+14d=3
Вычитаем из нижнего уравнения верхнее:
8d=-40 |÷8
d=-5 ⇒
a₁+6*(-5)=43
a₁-30=43
a₁=73
a₁₂=73+11*(-5)=73-55=18
ответ: a₁₂=18.
3. a₁=30 d=-0,4 a₁₂=?
a₁₂=30+11*(-0,4)=30-4,4=25,6
ответ: a₁₂=25,6.
4. a₁₀=9,5 S₁₀=50 a₁₂=?
Sn=(a₁+an)*n/2
(a₁+9,5)*10/2=50
(a₁+9,5)*5=50 |÷5
a₁+9,5=10
a₁=0,5
a₁₀=a₁+9d=9,5
0,5+9d=9,5
9d=9 |÷9
d=1 ⇒
a₁₂=a₁+11d=0,5+11*1=0,5+11=11,5.
ответ: а₁₂=11,5.
III. Формулювання мети і завдань уроку
Формулюємо проблему: як знайти значення виразу
.
де х1 і х2 – корені даного квадратного рівняння (не розв'язуючи рівняння)? Пошук відповіді на це запитання і вивчення сфери застосування теореми Вієта та теореми, оберненої до неї (вдосконалення вмінь), — основна мета уроку.
IV. Актуалізація опорних знань та вмінь
Виконання усних вправ
1. Замініть рівняння рівносильним йому зведеним квадратним рівняння:
а) 3х2 – 6х – 9 = 0; б) 2у2 + у – 7 = 0; в) х2 – 3х + 1,5 = 0
та знайдіть суму і добуток його коренів.
2. Наведіть приклад квадратного рівняння, в якого:
а) один корінь дорівнює нулю, а другий — не дорівнює нулю;
б) обидва корені дорівнюють нулю;
в) немає дійсних коренів;
г) корені — протилежні ірраціональні числа.
3. Один із коренів квадратного рівняння х2 + 4х – 21 = 0 дорівнює