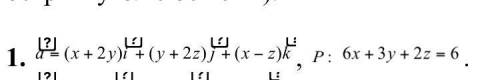
Биквадратное уравнение.
Решается заменой переменной:

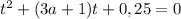
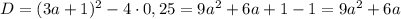
Если D >0, т.е.


уравнение имеет корни:
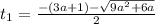 или
или 
Обратный переход:
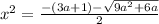 или
или 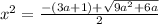
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
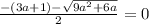
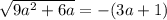
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Аналогично
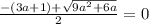
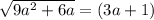
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Если  , т.е
, т.е 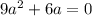
 или
или 
При 
уравнение принимает вид:

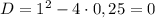 ⇒
⇒ 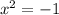
уравнение не имеет корней
При 
уравнение принимает вид:

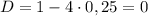 ⇒
⇒ 
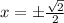
Уравнение 4-ой степени, значит
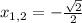 и
и 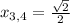
О т в е т. При 
Время, за которое первый лыжник преодолел расстояние в 40 км будет:
40/(х-2)=t
Второй лыжник потратил столько же времени, сколько и первый, только преодолел 48 км, его время будет:
48/х=t
Т.к. время первого и второго лыжников равны, получаем уравнение:
t=40/(х-2)=48/х
Решаем это уравнение относительно х:
40 = 48
х-2 х
40*х=48*(х-2)
40х=48х-48*2
40х=48х-96
48х-40х=96
8х=96
х=96:8
х=12 км/ч - скорость второго лыжника.
Скорость первого лыжника на 2 км/ч меньше, чем у второго, т.е.:
12-2=10 км/ч - скорость первого лыжника.