Объяснение:
Чтобы решить эту задачу, нужно знать как минимум 2 операции с матрицами:
Сложение/вычитание матриц. Если у тебя есть матрица A с элементами
(т.е. на i строке j столбца находится число ), и некоторая другая матрица той же размерности B с элементами 
, то в итоговой матрице C = A + B элементы 
, с вычитанием все то же самое, только разность a и b. На практике это выглядит как сумма (или разность) соответствующих чиселУмножение матриц на некоторую константу. Если умножать матрицу A с элементами на некоторое постоянное число C, то C*A =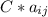 
, т.е. умножаете это число на каждый элемент матрицы.Теперь давайте найдем по условию 3A
![3A = \left[\begin{array}{cc}12&-3\\9&6\end{array}\right]](/tpl/images/0988/6779/046d9.png)
Теперь 2B:
![2B = \left[\begin{array}{cc}-4&2\\10&6\end{array}\right]](/tpl/images/0988/6779/f0fc3.png)
Теперь поэлементно из одного вычитаем другое:
![C = 3A - 2B = \left[\begin{array}{cc}16&-5\\-1&0\end{array}\right]](/tpl/images/0988/6779/e2957.png)
В решении.
Объяснение:
Решить квадратные уравнения:
1) х²-х-6= 0
D=b²-4ac =1+24=25 √D= 5
х₁=(-b-√D)/2a
х₁=(1-5)/2
х₁= -4/2
х₁= -2;
х₂=(-b+√D)/2a
х₂=(1+5)/2
х₂=3.
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
2) х²+3х=4
х²+3х-4 =0
D=b²-4ac =9+16=25 √D= 5
х₁=(-b-√D)/2a
х₁=(-3-5)/2
х₁= -8/2
х₁= -4;
х₂=(-b+√D)/2a
х₂=(-3+5)/2
х₂=2/2
х₂=1.
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
3) х²=2х+8
х²-2х-8 =0
D=b²-4ac =4+32=36 √D= 6
х₁=(-b-√D)/2a
х₁=(2-6)/2
х₁= -4/2
х₁= -2;
х₂=(-b+√D)/2a
х₂=(2+6)/2
х₂=8/2
х₂=4.
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
4) 25х²-1=0 (неполное квадратное уравнение).
25х² = 1
х² = 1/25
х = ±√1/25
х₁ = -1/5;
х₂= 1/5.
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.
Объяснение:
Во-первых, 3 чайных розы можно сразу отложить в сторону, их не хватит на букет, потому что нужно 5 роз.
Остается 12 белых и 20 красных роз.
Если все розы одного цвета одинаковы, то ответ 2 - или 5 белых, или 5 красных, и больше тут думать нечего.
Если же все розы разные, то нужно считать сочетания:
C(5, 12) = (12*11*10*9*8)/(1*2*3*4*5) = 11*9*8 = 792 белых букета.
C(5, 20) = (20*19*18*17*16)/(1*2*3*4*5) = 19*3*17*16 = 15504 красных букета.
Всего 792 + 15504 = 16296 букетов.