3y - |2x - 6| = 0,
3y - |2·(x-3)| = 0,
3y - |2|·|x-3| = 0,
3y - 2·|x-3| = 0,
При x-3≥0 ⇔ x≥3 имеем |x-3| = x-3, тогда
3y - 2·(x-3) = 0,
3y - 2x + 6 = 0,
3y = 2x-6,
y = (2/3)·x - 2.
При x-3<0 ⇔ x<3 имеем |x-3| = - (x-3) = -x+3, тогда
3y - 2·(-x+3) = 0,
3y + 2x - 6 = 0,
3y = -2x + 6,
y = -(2/3)·x + 2.
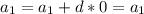проверено.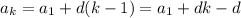
![a_{k+1}=a_1+d[(k+1)-1]=a_1+dk](/tpl/images/0582/6750/35dc7.png)
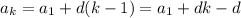то прибавив к данному выражению d. Мы получим следующий член .![S_n= \frac{n[2a_1+d(n-1)]}{2}](/tpl/images/0582/6750/67d86.png)
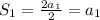. ![n=k \Rightarrow S_k= \frac{k[2a_1+d(k-1)]}{2}= \frac{2a_1k+dk^2-dk}{2}](/tpl/images/0582/6750/b9ca4.png)
:
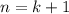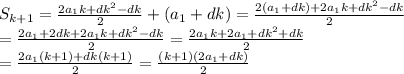
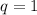получается деление на ноль, поэтому сразу пишем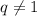 
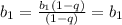
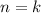
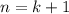:![b_{k+1}= \frac{b_1(1-q^k)}{1-q}+b_1q^k= \frac{(1-q)b_1q^k+b_1(1-q^k)}{1-q}\\= \frac{b_1[(1-q)q^k+(1-q^k)]}{1-q}= \frac{b_1[q^k-q^{k+1}+1-q^k]}{1-q}= \frac{b_1(1-q^{k+1})}{1-q}](/tpl/images/0582/6750/552be.png)
Первое уравнение - график окружности с центром в точке (0;0), то есть в начале координат, радиусом 3.
Второе уравнение y=x^2+p, график параболы, ветви которой направлены вверх, и которая двигается по оси Oy вверх или вниз(но не влево и вправо) в зависимости от значения p. Парабола будет иметь с графиком окружности 3 точки пересечения (а значит и система будет иметь три решения), когда вершина параболы будет лежать на окружности, а две ветви параболы будут пересекать окружность в 2 точках. Вершина параболы должно лежать в точке (0; -3) чтобы это выполнялось, а значит p=-3
P.S. если что-то не понятно, напишите.
Если правильно понял вопрос, то нужно раскрыть модуль при x < 3. По определению модуль - это расстояние, всегда положительное число. Очевидно, что |x| = -x при x < 0. В случае, когда имеем выражение в модуле, можно просто провести замену: z = 2x-6. Тогда понимая, что при x < 3, 2x-6 < 0 то же, что и z < 0. Значит |z| = -z = -(2x - 6) = -2x + 6. А дальше просто построить график. Конечно, делать замену для модуля не нужно. Просто нужно понимать, что можно просто менять знаки перед каждым слагаем, что и получилось в записи -z = -(2x - 6)