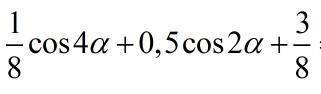
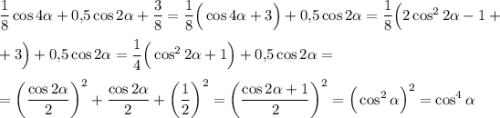
ответ:сos⁴α
Объяснение:(1/8)*(2cos²2α-1)+(1/2)cos2α+3/8=(1/4)(cos²2α+1+2cos2α)
=(1/4)(cos2α+1)²=(2cos²α-1+1)²/4=cos⁴α
 на одну единицу вверх вдоль (параллелно) оси OY. График "поднимается" .
на одну единицу вверх вдоль (параллелно) оси OY. График "поднимается" .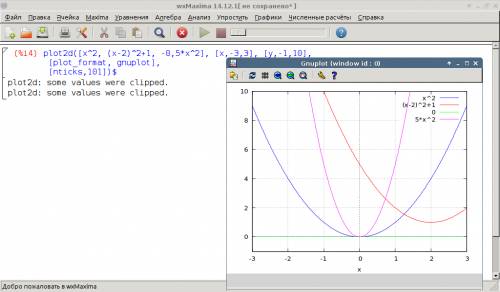
 . Понизим порядок:
. Понизим порядок: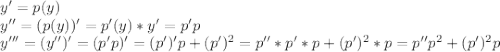 (1)
(1)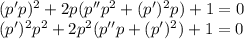 .
.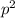 (
(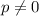 , в противном случае мы бы имели уравнение
, в противном случае мы бы имели уравнение 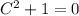 , нерешаемое в действительных числах):
, нерешаемое в действительных числах):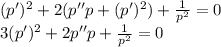 .
.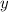 . Сделаем замену
. Сделаем замену 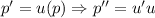 . Тогда:
. Тогда: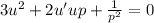 , или, полагая
, или, полагая 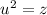 ,
,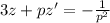 .
.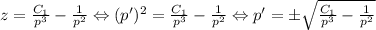
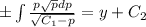 (2)
(2)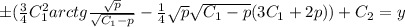 (1')
(1')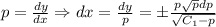 , отсюда, находя интеграл в правой части, находим
, отсюда, находя интеграл в правой части, находим 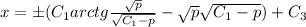 . (2')
. (2')