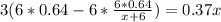
18 литров.
Объяснение:
Смотри решение на фото

Производная y' = (3х + 4 )' = 3 + 0,5·4 ·(-2x)/
)' = 3 + 0,5·4 ·(-2x)/ = 3 - 4x/
= 3 - 4x/ ;
;
y' = 0 if 3 - 4x/ = 0, (-1 < x < 1) ⇒ 4x = 3
= 0, (-1 < x < 1) ⇒ 4x = 3 ⇔ (обе части
⇔ (обе части
возводим в квадрат при условии x ≥ 0) ⇔ 16х² = 9 - 9х² ⇒ 25х² = 9 ⇒
х₁₂ = ± √9/√25 = ± 3/5. Отрицательный корень откидываем ⇒
х = 3/5 - стационарная точка. При (х = 0,8 > 3/5) y' = 3 - 4*0,8/√0,64 =
3 - 16/3 = - 7/3 < 0 ⇒ х = 3/5 - точка максимума исходной функции, и в ней у принимает наибольшее значение ⇒ Y наиб. = у(3/5) = 9/5 + 4*0,8 = 5; наименьшее значение функции будем искать на концах отрезка [-1; 1]:
y(1) = 3 + 4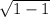 = 3, y(-1) = -3 + 4
= 3, y(-1) = -3 + 4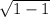 = -3 ⇒ Y наименьшее = y(-1) = -3 ⇒
= -3 ⇒ Y наименьшее = y(-1) = -3 ⇒
Y наиб. + Y наименьшее = -3 + 5 = 2. ответ: А) 2
ответ: за 90 с.
Объяснение:
Пусть v0 м/с - скорость эскалатора относительно неподвижного наблюдателя и v1 м/с - скорость Вовы относительно эскалатора. Тогда скорость Вовы относительно неподвижного наблюдателя v2=v0+v1 м/с. Пусть l м - длина эскалатора, тогда по условию:
l/v2=l(v0+v1)=40
l/v0=72
Если бы эскалатор был неподвижен, то Вова преодолел бы его за время t=l/v1 с. Разделив второе уравнение системы на первое, приходим к уравнению (v0+v1)/v0=72/40=9/5. Оно приводится к виду 1+v1/v0=9/5, откуда v1/v0=4/5=0,8. Отсюда v1=0,8*v0 и тогда t=l/v1=l/(0,8*v0)=1,25*l/v0=1,25*72=90 с.
Пусть х литров воды было в сосуде, добавили 6 литров спирта, значит в сосуде ( x+6) литров раствора, в котором 0,64·6=3,84 л чистого спирта.
Процентное содержание спирта:
(х+6) л составляет 100%
3,84 л составляют p%
Выливаем 6 литров, т. е в сосуде остается
х л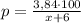 % раствора
% раствора
Значит,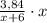 л чистого спирта
л чистого спирта
Повторяем процедуру три раза
1)
Доливаем первый 6 литров 64% спирта.
Получаем:
(х+6) л раствора, в котором
Выливаем 6 литров, т. е в сосуде остается
х л раствора, в котором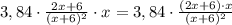 л чистого спирта.
л чистого спирта.
2)
Доливаем второй раз 6 литров 64% спирта.
Получаем:
(x+6) л раствора, в котором
л чистого спирта.
...