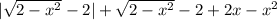 ?
?объяснение:
№5 если в выпуклом четырёхугольнике диагонали равны и равны две противоположные стороны, то по признаку он или прямоугольник, или квадрат, или равнобокая трапеция.
в прямоугольнике и в квадрате диагонали,пересекаясь, делятся пополам, ⇒ ао=до, как половины равных отрезков.
если имеем равнобокую трапецию,то из равенства треугольников, имеющих своими сторонами основание ад и диагонали, получим равные угла между диагоналями и основанием ад ⇒δаод- равнобедренный и ао=од (замечание: чертёж, представленный в неверен, т.к. диагонали преломляются).
№6. т.к. противоположные стороны попарно равны ⇒ четырёхугольник - параллелограмм по признаку ⇒ диагонали точкой пересечения делятся пополам по свойству диагоналей параллелограмма.
короче тут надо по плану все сделать короче первое:рисуешь график,2.План:1.х+3 рисуешь х на графике а потом смещаешь вправо на 3 единицы.2.потом пишешь систему переписуешьпотом тебе надо выразить эти два уравнения через х и делаешь замену у на "а" а х на "б" и решаешь потом то чо получится расписывашь по формлуе упрощенного умножения
Объяснение:
короче тут надо по плану все сделать короче первое:рисуешь график,2.План:1.х+3 рисуешь х на графике а потом смещаешь вправо на 3 единицы.2.потом пишешь систему переписуешьпотом тебе надо выразить эти два уравнения через х и делаешь замену у на "а" а х на "б" и решаешь потом то чо получится расписывашь по формлуе упрощенного умножения
Раскроем модуль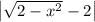 по правилу:
по правилу: 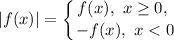
Если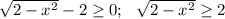
Таким образом, может быть только отрицательным.
может быть только отрицательным.
Если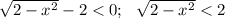
Следовательно,
Имеем квадратичную функцию, графиком которой является парабола, с ветвями, направленными вниз.
У такой функции наибольшим значением будет вершина параболы, а наименьшим — на ее концах из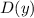 .
.
Определим абсциссу вершины параболы:
Определим ординату вершины параболы:
Таким образом, наибольшим значением функции на отрезке![\left[-\sqrt{2}; \ \sqrt{2} \right]](/tpl/images/1358/3129/99aa4.png) будет
будет 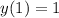
Определим значение функции на концах отрезка![\left[-\sqrt{2}; \ \sqrt{2} \right]](/tpl/images/1358/3129/99aa4.png)
ответ:![\displaystyle \max_{[-\sqrt{2}; \ \sqrt{2}]}y = y(1) = 1; \ \displaystyle \min_{[-\sqrt{2}; \ \sqrt{2}]}y = y(-\sqrt{2}) = -2\sqrt{2} - 2](/tpl/images/1358/3129/961a6.png)