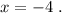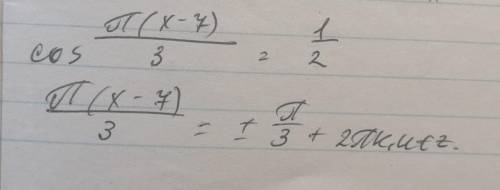

1) х² - 8х + 15 ≥ 0
Решаем уравнение
х² - 8х + 15 = 0
D = 8² - 4 · 15 = 4 = 2²
x₁ = 0.5(8 - 2) = 3
x₂ = 0.5( 8 + 2) = 5
Значения функции у = х² - 8х + 15 не отрицательны при х≤ х₁ и х≥ х₂
Неравенство имеет решение при х ∈ (-∞; 3] ∪ [5; +∞)
2) х² - 6х + 9 < 0
Преобразуем левую часть неравенства
(х - 3)² < 0
Квадрат любого числа неотрицателен, поэтому неравенство не имеет решений.
3) х² - 4х + 20 ≤ 0
Решаем уравнение
х² - 4х + 20 = 0
D = 4² - 4 · 20 = -64
Уравнение решений не имеет. Поэтому все значения функции у = х² - 4х + 20 положительны, и неравенство не имеет решений.
4) -х² + 7х - 12 < 0
Решаем уравнение
-х² + 7х - 12 = 0
D = 7² - 4 · 12 = 1
x₁ = -0.5(-7 + 1) = 3
x₂ = -0.5(-7 - 1) = 4
Значения функции у = -х² + 7х - 12 отрицательны при х > х₁ и х < х₂
Неравенство имеет решение при х ∈ (3; 4)
ответ.
Теперь, чтобы отобрать наибольший отрицательный корень, будем придавать "n" целые числовые значения.
При всех неотрицательных целых "n" и первая и вторая серии ответов дадут положительные значения "х" ("х" - корень уравнения).
Например, при n=0 получим в первой серии х=8+6*0=8>0 , а во второй серии х=6+6*0=6>0 ; при n=1 получим в первой серии х=8+6*1=14>0 , во второй серии х=6+6*1=12>0 ; при n=2 получим в первой серии х=8+6*2=20>0 , а во второй серии х=6+6*2=18>0 и т.д.
В задании спрашивают об отрицательных корнях. При неотрицательных значениях "n" отрицательные корни не получаются. Поэтому теперь будем придавать отрицательные значения "n".
При n= -1 получим в первой серии х=8+6*(-1)=2>0 , а во второй серии х=6+6*(-1)=0 .
При n= -2 получим в первой серии х=8+6*(-2)=-4<0 , а во второй серии х=6+6*(-2)= -6<0 .
При n= -3 получим в первой серии х=8+6*(-3)= -10<0 , а во второй серии х=6+6*(-3)= -12<0 .
И так далее. Значения корней "х" будут уменьшаться.
Мы получили такие значения "х":
Поэтому самое большое отрицательное значение корня "х" будет равно (-4) .
ответ: наибольший отрицательный корень - это