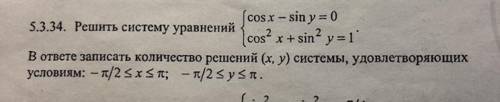
-√14; -3(1); 3,147.
Объяснение:
В данном примере трудность для сравнения представляют только 2 числа: -√14 и -3(1). Какое из них меньше?
Если мы точно не знаем, чему равен √14, то можно сравнить его с ближайшими квадратами чисел, которые мы знаем или легко можем рассчитать.
Ближайшие - это 3^2 = 9 и 4^2 = 16.
14 лежит в интервале от 9 до 16, но 5 единицах от 9 и всего в 2-х единицах от 16, - значит, √14 значительно больше половины интервала числе от 3 до 4, которые возводили в квадрат, т.е. √14 > 3,5.
Можем проверить: 3,5^2 = 12,25, а у нас 14.
Делаем вывод: - √14 на числовой оси лежит левее (то есть меньше) -3(1).
Таким образом, в порядке возрастания числа располагаются в следующем порядке:
-√14; -3(1); 3,147.
упростим второе с учетом первого. получим cos²x-cos²y=0⇒cosx=±cosy
cosy-siny=0;
sin(π/2-y)-siny-0;
2sin(π/4-y)*cosπ/4=0;
sin(π/4-y)=0; y=πn-π/4; n∈Z;
-π/2≤πn-π/4≤π; -1/2≤n-1/4≤1; 1/2≤n≤1 1/4; n=1; у=3π/4; n≤0; у= -π/4; Если у=3π/4; то x=3π/4 ±π; если у=-π/4, то х=-π/4±π
всего четыре корня. аналогично рассматривается случай cosx=-cosy