Часть А
Задание 1
а) (2а-а²)-(а²+2а-7) = 2а-а²+а²-2а+7 = 7
б) (1-у)3х²у-(3ху-х)ху = ху(3х-3ху-3ху+х) = ху(4х-6ху) = 2х²у (2-3у)
Задание 2
9^6 - 3^10 = 3^7 - 3^10 = 3^-3 : 24 = 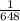
Задание 3
а) 27t²-3t = 0
3³t²-3t = 0
3²t = 0
9t = 0
t = 0
б) 4х²-2х-4х²+8х=4
6х = 4
х = 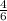 =
= 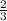
в) 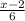 -
- 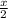 = 2
= 2
х-2 -3х = 12
-2х = 14
х = -7
Часть В
1) Пусть х деталей в час изготавливал ученик, тогда мастер -- (х+6) дет в час. Составляем уравнение по условию задачи:
8х=5(х+6)
8х=5х+30
8х-5х=30
3х=30
х=10 ( дет) в час изготавливал ученик
10+6=16 дет в час изготавливал мастер
Объяснение:
Подробное решение и есть объяснение, можно лучший ответ?
фнизу
Объяснение:
Выделяем множитель
2
из
4
cos
2
(
x
)
−
2
−
2
cos
(
x
)
.
Нажмите, чтобы увидеть больше шагов...
2
(
2
cos
2
(
x
)
−
1
−
cos
(
x
)
)
=
0
Разлагаем на множители.
Нажмите, чтобы увидеть больше шагов...
2
(
cos
(
x
)
−
1
)
(
2
cos
(
x
)
+
1
)
=
0
Разделим каждый член в выражении
2
(
cos
(
x
)
−
1
)
(
2
cos
(
x
)
+
1
)
=
0
на
2
.
2
(
cos
(
x
)
−
1
)
(
2
cos
(
x
)
+
1
)
2
=
0
2
Сократить общий множитель
2
.
Нажмите, чтобы увидеть больше шагов...
(
cos
(
x
)
−
1
)
(
2
cos
(
x
)
+
1
)
=
0
2
Делим
0
на
2
.
(
cos
(
x
)
−
1
)
(
2
cos
(
x
)
+
1
)
=
0
Если любой отдельный множитель в левой части уравнения равен
0
, то и все выражение будет равняться
0
.
cos
(
x
)
−
1
=
0
2
cos
(
x
)
+
1
=
0
Приравняем первый множитель к
0
и решим.
Нажмите, чтобы увидеть больше шагов...
x
=
2
π
n
,
2
π
+
2
π
n
для всех целых
n
Приравняем следующий множитель к
0
и решим.
Нажмите, чтобы увидеть больше шагов...
x
=
2
π
3
+
2
π
n
,
4
π
3
+
2
π
n
для всех целых
n
Итоговым решением являются все значения, обращающие
2
(
cos
(
x
)
−
1
)
(
2
cos
(
x
)
+
1
)
2
=
0
2
в верное тождество.
x
=
2
π
n
,
2
π
+
2
π
n
,
2
π
3
+
2
π
n
,
4
π
3
+
2
π
n
для всех целых
n
Объединяем ответы.
x
=
2
π
n
3
для всех целых
n
1) Рассмотрим команду (пусть это будет команда М), которая выиграла наименьшее количество встреч. Пусть это число равно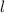 . Рассмотрим два случая:
. Рассмотрим два случая:
1.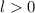 . Заметим, что количество побед этой команды равно количеству побежденных, а это число, в свою очередь, равно суммарному количеству побед побежденных. Очевидно, что каждый побежденный выиграл ровно 1 раз (если нет, то найдется хотя бы один побежденный с 0 побед, что противоречит минимальности). Значит,
. Заметим, что количество побед этой команды равно количеству побежденных, а это число, в свою очередь, равно суммарному количеству побед побежденных. Очевидно, что каждый побежденный выиграл ровно 1 раз (если нет, то найдется хотя бы один побежденный с 0 побед, что противоречит минимальности). Значит, 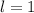 . Побежденный командой М тоже имеет 1 победу и так далее. Получим, что каждый победил ровно 1 раз. Поскольку каждый матч заканчивается чьей-то победой, то всего побед столько же, сколько и матчей. Суммарное количество побед равно
. Побежденный командой М тоже имеет 1 победу и так далее. Получим, что каждый победил ровно 1 раз. Поскольку каждый матч заканчивается чьей-то победой, то всего побед столько же, сколько и матчей. Суммарное количество побед равно 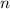 — числу участников (поскольку все победили 1 раз). Имеем:
— числу участников (поскольку все победили 1 раз). Имеем: 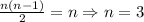 .
.
2.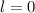 . Уберем команду М. Тогда количество побед каждой команды уменьшится на 1 (так как все победили команду М). Рассмотрим новую команду, имеющую наименьшее количество побед (
. Уберем команду М. Тогда количество побед каждой команды уменьшится на 1 (так как все победили команду М). Рассмотрим новую команду, имеющую наименьшее количество побед (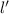 ). Если
). Если 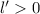 , то получим 3 команды + изъятая, то есть всего 4 команды. Если
, то получим 3 команды + изъятая, то есть всего 4 команды. Если  , то была команда с ровно одной победой. Продолжая рассуждения, получим, что была команда с хотя бы двумя победами, тремя и т.д. до
, то была команда с ровно одной победой. Продолжая рассуждения, получим, что была команда с хотя бы двумя победами, тремя и т.д. до  , то есть была команда, которая победила всех. Тогда
, то есть была команда, которая победила всех. Тогда 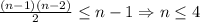 . Значит, могло быть либо три, либо четыре команды.
. Значит, могло быть либо три, либо четыре команды.
2) Пусть первая труба наполняет бассейн за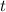 часов. Составим уравнение:
часов. Составим уравнение: 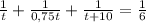 , откуда
, откуда 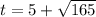 , остальные ищутся легко.
, остальные ищутся легко.