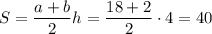Объяснение:
1. Дан правильный шестиугольник в котором вписана окружность с радиусом 2√3.
Формула:
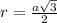
r-радиус вписанной окружности.
a-длина стороны шестиугольника.
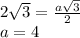
Сторона шестиугольника равна 4 см.
Периметр-сума всех сторон фигуры.
Так как у нас шестиугольник правильный то и все эго стороны равны.
Р-периметр.
Отсюда:
Р=6*а=6*4=24см
ответ: 24 см.
2. Диаметр равен 5,6 см. Найти длину окружности.
Формула:
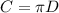
C-длина окружности.
π-число Пи.
D-диаметр.
С=π*5,6
С=5,6π см
ответ: 5,6π см
3.Радиус равен 12 см , градусная мера дуги равна 315°.Найти длину дуги окружности.
Формула:
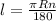
l-длина дуги.
R-радиус окружности.
n-градусная мера дуги.
π-число Пи.
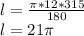
ответ: 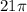 см.
см.
4.Длина дуги равна 20 см , градусная мера дуги равна 15°.Найти радиус окружности.
Формула:
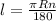
l-длина дуги.
R-радиус окружности.
n-градусная мера дуги.
π-число Пи (3,14)
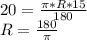
ответ: 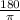 см.
см.
5.Градусная мера центрального угла равна 18° , радиус окружности равен 6 см. Найти площадь сектора.
Формула:
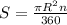
S-площадь сектора.
R-радиус окружности.
n-градусная мера дуги (центральный угол лежащий напротив дуги равен градусной мере дуги).
π-число Пи.
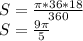
ответ: 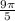 единиц квадратных.
единиц квадратных.
6.Сторона квадрата описанного над окружностью равна 18√6. Найти сторону треугольника вписанного в эту окружность.
Формула:
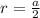 - радиус окружности вписанной в квадрат
- радиус окружности вписанной в квадрат
r-радиус окружности.
a-сторона квадрата.
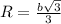
R-радиус той же окружности.
b-сторона треугольника.
Отсюда мы можем вывести формулу===>
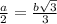
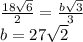
ответ: 27√2 см.
7.Внутрений угол правильного многоугольника равен 144°.Найти количество сторон многоугольника.
Формула:
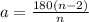
a-градусная мера внутреннего угла.
n-количество сторон в многоугольнике.
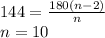
ответ: 10 сторон.
40
Объяснение:
Модули принимают значение 0, когда y = x² и y = -x². Начертим графики этих функций (синие, пунктирные). Они делят плоскость на 4 области. Рассмотрим, как раскрываются модули: "внутри" верхней параболы оба модуля раскрываются с плюсом (убеждаемся подстановкой точки x = 0, y = 1, оба подмодульных выражения положительны, обозначим как ++), "внутри" нижней — оба с минусом (подставляем x = 0, y = -1, обозначим как --), "снаружи" обеих парабол — первый с минусом, второй с плюсом (подставляем x = ±1, y = 0, обозначим как -+).
Рассмотрим разные случаи раскрытия модулей:
++: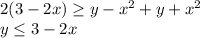
y = 3 - 2x — прямая, заключённая внутри верхней параболы. По неравенству нам подходит всё, что ниже этой прямой. Она пересекает параболу y = x² при x² = 3 - 2x ⇔ x² + 2x - 3 = 0 ⇔ x = -3; 1.
--: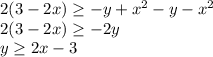
y = 2x - 3 — прямая, заключённая внутри нижней параболы. По неравенству подходит всё, что выше этой прямой. Она пересекает параболу y = -x² при -x² = 2x - 3 ⇔ x² + 2x - 3 = 0 ⇔ x = -3; 1.
-+: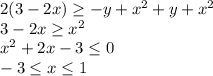
x = -3; 1 — это две вертикальные прямые, заключённые между параболами (в области -+). По неравенству подходит всё, что между ними. Они пересекаются с параболами в тех же точках, что и прямые.
Красным обозначим полученные отрезки. Из предыдущих рассуждений получаем, что нам подходит всё, что внутри красной фигуры. Эта фигура — трапеция, так как её основания (вертикальные прямые x = -3; 1) параллельны и не равны (длина первого отрезка — 2·(-3)² = 18, длина второго — 2·1² = 2, умножаем на 2 в силу симметрии графиков y = x² и y = -x² относительно Ox). Высота — расстояние между этими прямыми, то есть 1 - (-3) = 4. Площадь трапеции равна