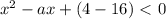 не имеет решение
не имеет решениерассмотрим квадратный трехчлен х²-ах+(4а-16), его первый коэффициент равен 1, а дискриминант D=а²-4*1*(4а-16)=а²-16а+64=(а-8)²
т.к. графиком квадратичной функции у= х²-ах+(4а-16) является парабола, ветви которой направлены вверх, то неравенство
х²-ах+(4а-16) <0 не будет иметь решений, когда парабола будет находиться выше оси ох, или будет касаться оси ох, а это достигается, когда дискриминант меньше нуля или равен нулю, но (а-8)²≥0 при любом значении а, значит, при а=8 неравенство не имеет решения.
ответ при а=8.
Чокан Валиханов был чингизидом — правнуком Абылай-хана. Дед Чокана Вали-хан — один из 30 сыновей Абылай-хана. Чокан Валиханов родился в орде-зимовке Кунтимес Аманкарагайского внешнего округа (ныне аул Кунтимес в Сарыкольском районе Костанайской области). Кунтимес была постоянной зимовкой 1834—1853 гг. его отца Чингиса Валиханова[10], старшего султана Аманкарагайского (с 1845 г. Кушмурунского) округа Омской области. При рождении мальчику было дано мусульманское имя Мухаммед-Канафия. Позже придуманное его прозвище Чокан закрепилось как официальное имя. В детстве (1842—1847 гг.) мальчик учился в казахской школе, открытой в орде Кунтимес, где он получил начальные знания казахского, кыпшак-чагатайского, арабского и персидского языков.
9x2 + 3x; б) 6xy +3x2y – 12xy2
2°. Разложите на множители:
а) y(у – 1) + 2(y – 1); б) x2 – 64.
3°. Сократите дробь (x^2+ 3x)/(3a+ax).
4°. У выражение (а – b)2 – (а – b)(а + b).
5°. Решите уравнение x2 + 7x = 0.
6 У выражение: с(с – 2)(с + 2) – (с – 1)(с2 + с + 1).
7 Найдите корни уравнения 3x3 – 27x = 0.
8 Разложите на множители многочлен 2х + 2у – х2 – 2ху – у2.
2 вариант.
1°. Вынесите общий множитель за скобки:
а) 2ab – ab2; б) 5a4 – 10a3 + 10a2
2°. Разложите на множители:
а) ax – ay + 2x – 2y; б) 9a2 – 16b2.
3°. Сократите дробь (2a+4)/(a^(2 )- 4).
4°. У выражение (x – 1) (x + 1) – x(x – 3).
5°. Решите уравнение x2 – 25 = 0.
6 У выражение: (х + 1)(х2 + х + 1)
Объяснение:
a=8
Объяснение:
x²-ax+(4a-16)<0
Допустим:
x²-ax+(4a-16)=0
D=a²-4·(4a-16)=a²-16a+64=(a-8)²
x₁=(a-a+8)/2=4
x₂=(a+a-8)/2=a-4
a-4<x<4; a<8
4<x<a-4; a>8
Отсюда следует, что неравенство не имеет решений при a=8.