Question

Найдите наибольшую площадь трапеции, если три ее стороны равны а

Answer 1

Рассмотрим трапецию ABCD.

Основания трапеции не могут иметь одинаковую длину, так как в противном случае это будет параллелограмм. Значит, одно из оснований  BC и две боковые стороны AB и CD равны по а. Заметим, что рассматриваемая трапеция равнобедренная.

Проведем высоты BH и CK. Тогда, HK=а.

Обозначим AH=KD=х.

Высоту трапеции найдем по теореме Пифагора:

$BH=\sqrt{a^2-x^2}$

Запишем выражение для площади трапеции:

$S=\dfrac{BC+AD}{2}\cdot BH$

$S=\dfrac{BC+(AH+HK+KD)}{2}\cdot BH$

$S=\dfrac{a+(x+a+x)}{2}\cdot \sqrt{a^2-x^2}$

$S=\dfrac{2a+2x}{2}\cdot \sqrt{a^2-x^2}$

$S= (a+x)\cdot\sqrt{a^2-x^2}$

Исследуем на экстремумы функцию S. Найдем производную:

$S'= (a+x)'\cdot\sqrt{a^2-x^2}+(a+x)\cdot(\sqrt{a^2-x^2})'$

$S'=1\cdot\sqrt{a^2-x^2}+(a+x)\cdot\dfrac{1}{2\sqrt{a^2-x^2}} \cdot(a^2-x^2)'$

$S'=\sqrt{a^2-x^2}+(a+x)\cdot\dfrac{-2x}{2\sqrt{a^2-x^2}}$

$S'=\dfrac{2(a^2-x^2)-2x(a+x)}{2\sqrt{a^2-x^2}}$

$S'=\dfrac{2a^2-2x^2-2ax-2x^2}{2\sqrt{a^2-x^2}}$

$S'=\dfrac{-4x^2-2ax+2a^2}{2\sqrt{a^2-x^2}}$

Найдем нули производной:

$\dfrac{-4x^2-2ax+2a^2}{2\sqrt{a^2-x^2}}=0$

$-4x^2-2ax+2a^2=0$

$2x^2+ax-a^2=0$

$D=a^2-4\cdot2\cdot(-a^2)=a^2+8a^2=9a^2$

$x=\dfrac{-a-3a}{2\cdot2}=-a$

$x=\dfrac{-a+3a}{2\cdot2}=\dfrac{a}{2}$

При переходе через точку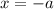 $x=-a$ производная меняет знак с минуса на плюс, значит это точка минимума.

При переходе через точку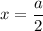 $x=\dfrac{a}{2}$ производная меняет знак с плюса на минус, значит это точка максимума.

Таким образом, наибольшую площадь трапеция имеет при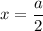 $x=\dfrac{a}{2}$. Эта площадь равна:

$S\left(\dfrac{a}{2}\right)= \left(a+\dfrac{a}{2}\right)\cdot\sqrt{a^2-\left(\dfrac{a}{2}\right)^2}= \dfrac{3a}{2}\cdot\sqrt{a^2-\dfrac{a^2}{4}}=\dfrac{3a}{2}\cdot\sqrt{\dfrac{3a^2}{4}}=\dfrac{3\sqrt{3} }{4}a^2$

ответ: $\dfrac{3\sqrt{3} }{4}a^2$