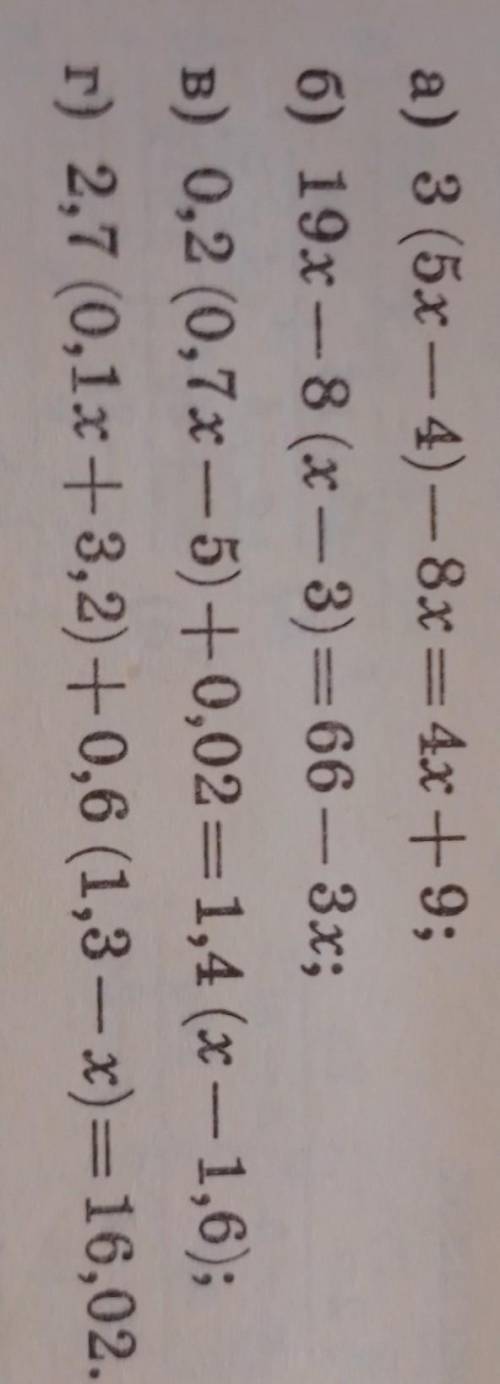
Объяснение:
а) 15х-12-8х=4х+9 3х=21 х=7
б)19х-8х+24=66-3х 14х=42 х=3
в)0,14х-1,4х=1-2,26 -1,26х=-1,26 х=1
г)0,27х+8,64+0,78-0,6х=16,02 -0,33х=6,6 х=-20
Периметр — сумма длин всех сторон.
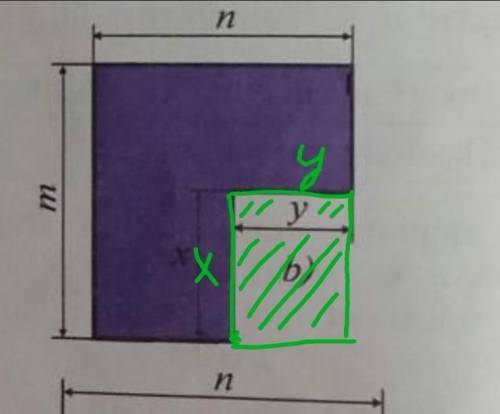
b) P = m + n + (m - x) + y + x + (n - y) = m + n + m - x + y + x + n - y = 2m + 2n
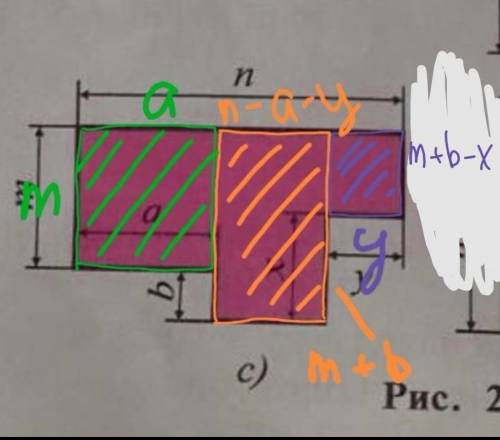
c) P = m + n + ((m + b) - x) + y + x + (n - a - y) + b + a = m + n + m + b - x + y + x + n - a - y + b + a = 2m + 2n + 2b
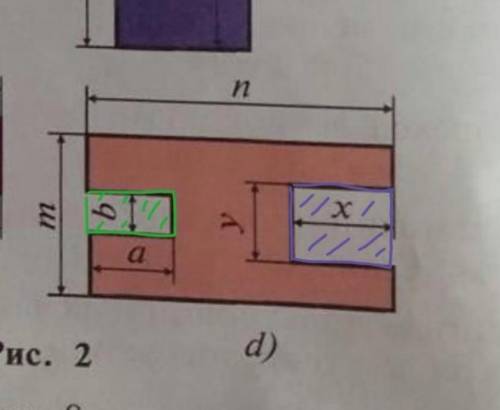
d) P = n + (m - y) + x + y + x + n + (m - b) + a + b + a = n + m - y + x + y + x + n + m - b + a + b + a = 2n + 2m + 2x + 2a
Площадь.
b) из площади общей фигуры вычтем площадь нижнего "прямоугольника". <приложение3>
S = (m × n) - (x × y) = mn - xy
с) разбиваем на три прямоугольника, площадь которых находится произведением смежных сторон. <приложение1>
S = (m × a) + ((n - a - y) × (m + b)) + (y × (m + b - x)) = am + nm + bn - am - ab - my - by + my + by - xy = nm + bn - ab - xy
d) из площади общей фигуры вычтем площади "вырезов". <приложение2>
S = (m × n) - (a × b) - (x × y) = mn - ab - xy
Дан треугольник с вершинами A(-4; 0), B(4:0), C(0; 2).
Так как точки даны на осях, то легко определяем длины сторон его.
АВ = 4-(-4) = 8.
АС = ВС = √(4² + 2²) = √(16 + 4) = √20 = 2√5.
Определяем радиус описанной окружности:
R = (abc)/(4S).
Площадь треугольника S = (1/2)*AB*H = (1/2)*8*2 = 8 кв.ед.
Тогда R = (2√5*8*2√5)/(4*8) = 5.
Теперь можно разложить вектор DC по векторам DA и DB, построением параллелограмма.
Проводим диагональ FG.
Из подобия треугольников DOB и DHG находим:
DG = (3/5)DB, DF = (3/5)DA.
Но так как DA = DB, то DG = DF.
ответ: DC = (3/5)(DA + DB).

а) 3(5x-4)-8x=4x+9
15x-12-8x=4x+9
3x=21
x=7
б) 19x-8(x-3)=66-3x
19x-8x+24=66-3x
14x=42
x=3
в) 0,2(0,7x-5)+0,02=1,4(x-1,6)
0,14x-1+0,02=1,4x-2,24
1,26x=1,26
x=1
г) 2,7(0,1x+3,2)+0,6(1,3-x)=16,02
0,27x+8,64+0,78-0,6x=16,02
-0,33x=6,6
x=-20