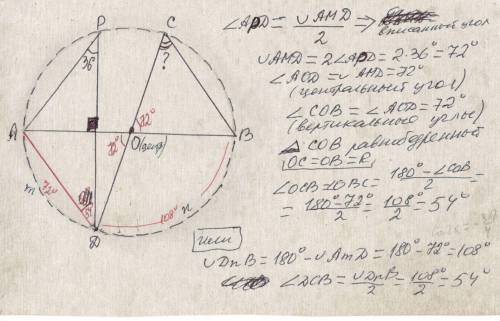
Найти угол DCB, когда AB и CD - диаметры окружности , ∠APD =36°
O центр окружности
ответ: 54°
Объяснение: см приложение
Если я правильно понял задание то:
Составим векторы c1 и c2 для этого вместо а и b подставим значения координат векторов приведенных в задании и руководствуясь правилами умножения и сложения векторов получим
![c1=2*\left[\begin{array}{c}-9\\5\\3\end{array}\right]-\left[\begin{array}{c}7\\1\\-2\end{array}\right] c2 = 3* \left[\begin{array}{c}-9\\5\\3\end{array}\right]+5*\left[\begin{array}{c}7\\1\\-2\end{array}\right]](/tpl/images/0065/4758/31ddd.png)
Получаем Необходимым и достаточным условие коллинеарности двух векторов является равенство нулю их векторного произведения
векторное произведение [a,b] для произвольных векторов а=(а1,а2,а3) и b=(b1,b2,b3) вычисляется по формуле
[a,b]={a2*b3-a3*b2; a3*b1-a1*b3; a1*b2-b1*a2}
Вычисляя по этой формуле векторное произведение c1 и с2 получаем:
[c1,c2]={-169; 39; -572} он не равен нулевому вектору, значит вектора не коллинеарны Векторы будут коллинеарны тогда и только тогда, когда существует такая константа m, что с1=m*c2
чтобы выяснить ее существование рассмотрим соотношение соответсвующих координат векторов c1 и с2
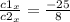
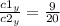
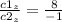
Получаем что:
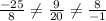
Значит такой константы m не существуют, векторы не коллинеарны
Объяснение:
Чтобы решить эту задачу, нужно знать как минимум 2 операции с матрицами:
Сложение/вычитание матриц. Если у тебя есть матрица A с элементами
(т.е. на i строке j столбца находится число ), и некоторая другая матрица той же размерности B с элементами 
, то в итоговой матрице C = A + B элементы 
, с вычитанием все то же самое, только разность a и b. На практике это выглядит как сумма (или разность) соответствующих чиселУмножение матриц на некоторую константу. Если умножать матрицу A с элементами на некоторое постоянное число C, то C*A =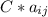 
, т.е. умножаете это число на каждый элемент матрицы.Теперь давайте найдем по условию 3A
![3A = \left[\begin{array}{cc}12&-3\\9&6\end{array}\right]](/tpl/images/0988/6779/046d9.png)
Теперь 2B:
![2B = \left[\begin{array}{cc}-4&2\\10&6\end{array}\right]](/tpl/images/0988/6779/f0fc3.png)
Теперь поэлементно из одного вычитаем другое:
![C = 3A - 2B = \left[\begin{array}{cc}16&-5\\-1&0\end{array}\right]](/tpl/images/0988/6779/e2957.png)
Дуга A(D)B = 180° (так как ограничена диаметром)
Угол APD - вписаный, значит, его градусная мера составляет половину от градусной меры дуги, на которую он опирается.
Дуга AD = 36*2 = 72°
Дуга DB = дуга A(D)B - дуга AD = 180° - 72° = 108°
Угол DCB - вписаный, значит, его градусная мера составляет половину от градусной меры дуги, на которую он опирается.
∠DCP = 108° : 2 = 54°