х²+bх-15=0
x1=3
Найти: х²
Для начала найдем b. Для этого подставим вместо переменной х ее первое значение:
3²+3b-15=0
3b=6
b=2
Теперь найдем второе значение х:
х²+2x-15=0
D=4+60=64
x²=-2-√64/2=-5
ответ: второй х равен -5.
1. Упростите выражение (2b + a) · (a - 2b) - (2b + a)² и найдите его значение, если a = -0,5 , b = 2.
(2b + a) · (a - 2b) - (2b + a)² = (a + 2b) · (a - 2b) - (4b² + 4ab + a²) = a² - 4b² - 4b² - 4ab - a² = - 8b² - 4ab ; a = -0,5 , b = 2 ⇒ - 8 · 2² - 4 · (-0,5) · 2 = - 8 · 4 + 2 · 2 = - 32 + 4 = - 28.
2. Докажите, что для любого n значение выражения (3n + 1)² - (3n - 1)² кратно числу 12.
(3n + 1)² - (3n - 1)² = ( 3n + 1 - (3n - 1) ) · (3n + 1 + 3n - 1) = 2 · 6n = 12n.
Так как результат умножения любого числа на 12 кратен 12, то значение выражения 12n кратно 12 при любых значениях переменной n, что и требовалось доказать.
В решении.
Объяснение:
1. Дано приведённое квадратное уравнение x²+px+q=0.
Что в нём означает коэффициент q?
х₁⋅х₂;
2. Дано приведённое квадратное уравнение x²+px+q=0.
Что в нём означает коэффициент p?
-х₁-х₂ = -(х₁+х₂);
3. Дано квадратное уравнение x²+12x−3,9=0, укажи сумму и произведение корней.
x₁+x₂= -12;
x₁⋅x₂= -3,9;
4. Составь квадратное уравнение, если известно, что его корни равны −4 и 1.
1) Найти р:
х₁ + х₂ = -р;
-4 + 1 = -3; значит, р = 3;
2) Найти q:
х₁ * х₂ = q;
-4 * 1 = -4; q = -4;
Уравнение:
z² + 3z − 4 = 0
5. Составь квадратное уравнение, корнями которого являются числа x₁= −9; x₂= −18, при этом коэффициент a=1.
1) Найти р:
х₁ + х₂ = -р;
-9 + (-18) = -27; значит, р = 27;
2) Найти q:
х₁ * х₂ = q;
-9 * (-18) = 162; q = 162;
Уравнение:
x² + 27x + 162 = 0.
6. Не используя формулу корней, найди корни квадратного уравнения x²+22x+85=0
x₁= -5; x₂= -17.
7. Найди корни квадратного уравнения x²+4x+3=0
x₁= -1; x₂= -3.
-5
Объяснение:
Если один из корней уравнения равен 3, то ты можем подставить его в уравнение. Зачем это нужно? Чтобы найти коэффициент b.
Мы нашли b. Теперь мы можем подставить его в исходное уравнение и уже ничего не сможет нам помешать его решить:
Воспользуемся теоремой Виета.
Получаем ответ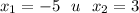
Второй корень нам известен, поэтому ответ на задачу -5