Пусть скорость пешехода х км/ч Тогда расстояние от А до В 3*х Время, затраченное им на обратный путь 16:х + (3х -16):(х-1) 16:х + (3х -16):(х-1) =3 +1/15 16:х + (3х - 16):(х-1) =46/15 умножим обе части уравнения на 15х(х-1), чтобы избавиться от дробей. 16*15(х-1) +15х (3х - 16)=46 х(х-1)240х-240 +45х²-240х=46х² -46х46х² -45х² -46х +240 =0 х² - 46х +240 =0D = b 2 - 4ac = 1156 √D = 34 х₁=40 ( не подходит для скорости пешехода) х₂=6 км/чS=vt=6*3=18 кмПроверка 16:6 + 2:5= 8/3+ 2/5= 40/15 +6/15=46/15=3 и 1/15 часа3 и 1/15 -3= 1/15 =4 минуты
Пусть пешеход из А до встречи х км Тогда второй, из В х км. Скорость первого, найденная по расстоянию от места встречи до пункта В, равна (3-х):12 км/минСкорость второго по расстоянию от места встречи до А равна х:48 км/минТак как пешеходы вышли одновременно, до встречи каждый из них шел одинаковое время:Первый шел х:((3-х):12)Второй шел (3-х):(х:48)Составим уравнение из равенства времени до места встречи:х:((3-х):12)=(3-х):(х:48)После некоторых преобразований и сокращения чисел уравнения на 36 получим квадратное уравнение х²-8х+12=0Корни этого уравнения ( решить сумеете его самостоятельно) 6 и 2. Первый корень не подходит, т.к. расстояние равно 3 км. ответ: пешеходы встретятся на расстоянии 2 км от пункта А. ( Можно решать, выразив время в часах: 48 мин=4/5 часа, 12 мин=1/5 часа)
а)
{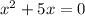
{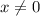
-------------------
{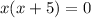
{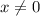
-------------------
{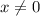
ответ : x = -5
б)
{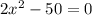
{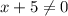
-------------------
{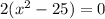
{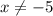
-------------------
{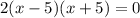
{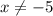
-------------------
{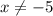
ответ : x = 5