Question

Пр32) Найдите наименьшее значение функции f(x)= 17/3x^2 + 75x^2/17 (используя производную)

$f(x) = \frac{17}{3 {x}^{2} } + \frac{75 {x}^{2} }{17 }$

Answer 1

$f(x) = \frac{17}{3x^2} + \frac{75x^2}{17} = \frac{17}{3}x^{-2} + \frac{75}{17}x^2\\(x^n)' = n*x^{n-1}\\f'(x) = \frac{17}{3}*(-2)*x^{-2-1} + \frac{75}{17}*2*x^{2-1} = \frac{150}{17}x - \frac{34}{3}x^{-3} = \frac{150}{17}x - \frac{34}{3x^3}\\ f'(x) = 0 = \frac{150}{17}x - \frac{34}{3x^3} = 0\\\frac{150}{17}x = \frac{34}{3x^3}\\450x^4 = 578\\x^4 = \frac{578}{450} = \frac{289}{225}\\x_1_,_2 = \pm\sqrt{\frac{17}{15} }\\-----(-\sqrt{\frac{17}{15} })+++(0)--(\sqrt{\frac{17}{15} })+++_x\\$

$f_{min} = f(\pm\sqrt{\frac{17}{15}}) = 10\\f_{max} = +\infty$

Answer 2

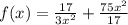
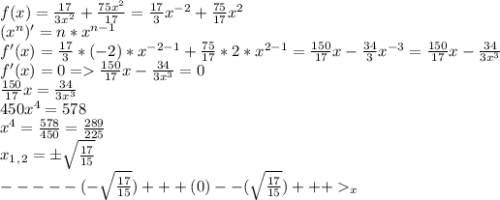
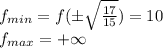
Найдем производную функции (17/3)*(-2х⁻³)+(150/17)*х

найдем критические точки  (17/3)*(-2х⁻³)+(150/17)*х=0

(17/3)*(-2х⁻³)+(150/17)*х=0

-17/(3х³)+(75х/17)/х=0; (-17*17+75*3х⁴)/х³=0;  (-17*17+75*3х⁴)/х³=0;

х⁴=17²/15²⇒х²=17/15; х=±√(17/15)

-√(17/15)___0√(17/15)

-                           +       -                         +

Т.к.  у нас получилось две точки минимума, и в них значение функции одинаково. то наименьшее значение равно f(-√(17/15))= (17/(3*17/15)+ (75(17/15))/17=5+5=10; f(√(17/15))= (17/(3*17/15)+ (75(17/15))/17=5+5=10

ответ 10