Слагаемые левой части представляют собой бесконечную геометрическую прогрессию с первым членом x и знаменателем x². Так как |x| < 1, x² < 1. Значит, это бесконечно убывающая геометрическая прогрессия, левую часть можно расписать по формуле :
Вектор, перпендикулярный плоскости 2x + 3y - 4z + 2 = 0 имеет координаты (2; 3; -4). Он обязательно будет лежать в плоскости, перпендикулярной данной, уравнение которой нам нужно составить. Отложим этот вектор, например, от точки A (-3; 2; 1), т. е. проведём вектор АС, который лежит в искомой плоскости. Получим точку С (-1; 5; -3), которая тоже лежит в искомой плоскости. Зная координаты трёх точек A (-3; 2; 1), В (4; -1; 2) и С (-1; 5; -3), лежащих в одной плоскости, найдём уравнение этой плоскости. Для этого составляем определитель: | x-(-3) 4-(-3) -1-(-3) | | y-2 -1-2 5-2 | = 0 | z-1 2-1 -3-1 |
0,5
Объяснение:
Слагаемые левой части представляют собой бесконечную геометрическую прогрессию с первым членом x и знаменателем x². Так как |x| < 1, x² < 1. Значит, это бесконечно убывающая геометрическая прогрессия, левую часть можно расписать по формуле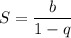 :
:
Из полученных корней подходит только x = 0,5.