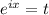Чтобы решить эту задачу, нам понадобятся два уравнения, одно из которых найдет значение меньшей стороны прямоугольника, а другое - большей стороны.
Пусть x - это меньшая сторона прямоугольника. Тогда большая сторона будет равна x + 6, так как она на 6 метров больше меньшей. Мы знаем, что площадь прямоугольника равна 160 м², поэтому мы можем записать уравнение площади:
x * (x + 6) = 160
Распространяем умножение:
x² + 6x = 160
Теперь приведем это уравнение к квадратному виду:
x² + 6x - 160 = 0
Для решения этого уравнения, можем воспользоваться формулой дискриминанта: D = b² - 4ac. В нашем случае, a = 1, b = 6 и c = -160. Подставим значения и посчитаем:
D = 6² - 4 * 1 * (-160) = 36 + 640 = 676
Дискриминант равен 676. Извлекаем квадратный корень из дискриминанта:
√676 = 26
Теперь воспользуемся формулой для нахождения корней квадратного уравнения: x = (-b ± √D) / 2a.
Давайте начнем сначала и пошагово нарисуем схематически графики функций, проработав каждую функцию отдельно:
1) Функция y = x в -0,75 степени
В данной функции основание (x) возведено в отрицательную степень (-0,75). Извлечение числа из отрицательной степени означает взятие корня из числа.
Найдем несколько значений функции для разных x, например x = 1, 2, 3 и т.д., и построим соответствующие точки на графике.
Пример:
Пусть x = 1. Тогда y = 1 в -0,75 степени, это означает взятие корня квадратного по модулю из 1, а затем обратить число в полученной степени.
y = 1 в -0,75 степени = 1 / √1 = 1 / 1 = 1
Таким образом, (1, 1) является одной из точек на графике функции y = x в -0,75 степени.
Повторим ту же процедуру для других значений x и добавим соответствующие точки на графике. После этого соединим все точки на графике гладкой кривой линией. Заметим, что график будет иметь форму параболы, открытой вниз.
2) Функция y = x в 15 степени
Аналогично предыдущей функции, проработаем несколько значений x и найдем соответствующие значения y для них.
Пример:
Пусть x = 1. Тогда y = 1 в 15 степени, это означает, что число 1 будет умножено на себя 15 раз.
y = 1 в 15 степени = 1 * 1 * 1 * 1 * 1 * 1 * 1 * 1 * 1 * 1 * 1 * 1 * 1 * 1 * 1 = 1
Таким образом, (1, 1) будет одной из точек на графике функции y = x в 15 степени.
Повторим эту процедуру для других значений x и добавим точки на график. Заметим, что график будет иметь форму кривой линии с резкими взлетами и падениями.
3) Функция y = x в -5 степени
Проделаем аналогичные шаги, чтобы найти некоторые значения функции и нарисовать график.
4) Функция y = x в 8 степени
Повторим вышеприведенные действия для этой функции.
5) Функция y = x в -6 степени
6) Функция y = x в корне из 3
7) Функция y = x в 9/11 степени
8) Функция y = x в 2 корень из 2
Проанализируйте каждую из этих функций, обратите внимание на их формы и свойства, и постарайтесь найти связь между формой функции и значениями параметра степени.
Весь процесс изображения графиков функций на бумаге поможет вам понять, как меняется форма графиков в зависимости от значений параметра степени.
Да, приведу самый простой пример:
Очевидно, что действительных решений тут нет.
Попробуем найти комплексные:
Сделаем замену :