Решение
Пусть скорость первого велосипедиста - x км/ч.
Тогда скорость второго - (x+3) км/ч.
Первый велосипедист проехал всё расстояние равное
36 км за (36/x) часов.
Второй проехал это расстояние за (36/(x+3)) часов.
Известно, что второй велосипедист проехал расстояние
на 1 час быстрее.
Составим уравнение:
36/x - 36/(x + 3) = 1
36(x + 3) - 36x = x(x + 3)
36x + 108 - 36x = x² + 3x
x² + 3x - 108 = 0
D = 9 + 4*108 = 441
x₁ = (- 3 + 21)/2 = 9
x₂ = (- 3 - 21)/2 =- 12 < 0 не удовлетворяет условию задачи
9 км/ч - скорость первого велосипедиста
1) 9 + 3 = 12 (км/ч) - скорость второго велосипедиста
ответ: 9 км/ч; 12 км/ч.
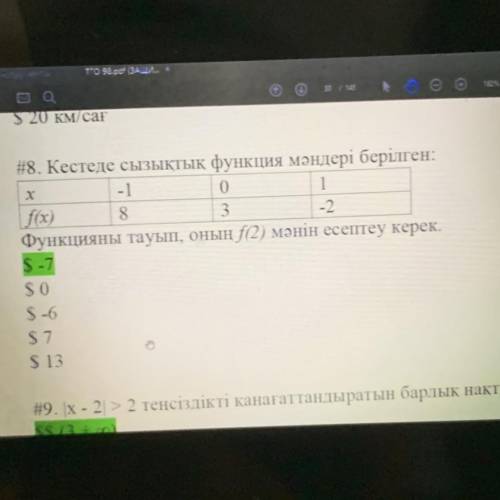
Здесь нужно по заданным точкам найти уравнение функции.
Возьмём функцию: у = k•x + b
Возьмём любые две известные нам точки. Например:
(0 ; 3) и (1 ; -2)
Обозначим:
х1 = 0 ; y1 = 3
x2 = 1 ; y2 = -2
По двум точкам можно найти угловой коэффициент (k) функции по формуле:
k = (y2-y1)/(x2-x1) = (-2-3)/(1-0) = -5.
Мы выяснили, что функция имеет вид:
у = -5x + b
Осталось только найти b. Это сделать очень легко. Просто подставим любую из данных точек в нашу функцию. Например: (0 ; 3)
у = -5х + b
3 = -5•0 + b
b = 3
Значит, функция имеет окончательный вид:
у = -5х + 3
f(x) = -5x + 3
Найдём f(2):
f(2) = -5•2 + 3 = -10 + 3 = -7
ответ: f(2) = -7.
Но можно также найти f(2) другим Он менее надёжен, но быстрей.
Вы можете увидеть, что каждый раз, когда значение аргумента (х) увеличивается на 1, значение функции (у) уменьшается на 5. Значит: f(2) = f(1) - 5 = -2 - 5 = -7 → ответ.
Удачи Вам и успехов)!