Question

137. Найдите сумму x+y если |x-4|+|3y-7|<=0​

Answer 1

|x - 4| + |3y - 7| ≤ 0

По скольку |x - 4| ≥ 0 и |3y - 7| ≥ 0  ( |x| ≥ 0) , то |x - 4| + |3y - 7| ≥ 0

Значит :

|x - 4| + |3y - 7| = 0

[ x - 4 = 0    =>    x = 4

[ 3y - 7 = 0    =>    3y = 7    =>    y = 7/3

x + y = 4 + 7/3 = 12/3 + 7/3 = 19/3

ответ : 19/3

Answer 2

$|x-4| + |3y-7| \leq 0$

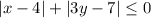
Сумма двух положительных (или нулевых) чисел не может быть меньше 0.

Значит, единственный вариант: 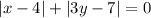$|x-4| + |3y-7| = 0$.

Это возможно только в том случае, если оба слагаемых = 0.

$\begin{cases}x - 4 = 0\\3y - 7 = 0\end{cases}$

$\begin{cases}x = 4\\y = \frac{7}{3}\end{cases}$

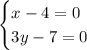
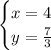
Значит 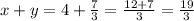$x + y = 4 + \frac{7}{3} = \frac{12 + 7}{3} = \frac{19}{3}$ - ответ.

================

Если решение удовлетворило, не забудь отметить его как "Лучшее".