примерно через 16 мин.
Объяснение:
Стрелки будут совпадать, когда минутная стрелка поравняется с часовой.
Минутная стрелка совершает один полный оборот за 1 час,
а часовая - за 12 часов.
1 ч = 60 мин
12 ч = 12 · 60 мин = 720 мин
Минутная стрелка за одну минуту сдвигается на 1/60 окружности циферблата, а часовая стрелка - на 1/720 окружности циферблата.
Найдём скорость сближения стрелок за одну минуту:
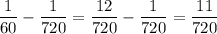 - (окружности циферблата).
- (окружности циферблата).
В 3 часа угол между часовой и минутной стрелками составляет 1/4 окружности.
Найдём через сколько минут стрелки встретятся:
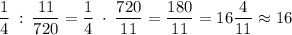
Відповідь:
Пояснення:
Решаем, используя геометрическое определение вероятности
S○=pi×R^2, где R=1 → S○=pi
а) более, ето строгое >
Рассмотрим точки , которие рассположени до 0,5.
удовлетворяют точки, расположенние от центра на растояниии от 0 до 0.5
r=0.5
S●=pi×(r)^2=0.5^2 pi=0.25рі
P=S●/S○=0.25pi/pi=0.25
Тогда искомая вероятнось
Р(растояние> 0,5)=1-0.25=0.75
б) рассмотрим точки, которие удалени на 0.3 и больше. необходимие точки находятся в круге с радиусом от 0.3 до 1.
Поетому S●=pi×(R^2-r^2)=(1-0.09)pi=0.91рі
P=0.91pi/pi=0.91
Поетому
Р(растояние <0.3)=1-0.91=0.09
Часы обыкновенные - это окружность, градусная мера 360
В три часа градусная мера 360/12 * 3 = 90
Рассчитаем градусную меру стрелок за час
Минутная - 360
часовая 360/12 = 30
За минуту часовая стрелка перемещается на:
30/60 = 0,5
Минутная стрелка на:
360/60 = 6
Значит разница скорости минутной и часовой стрелки составит:
6 - 0,5 = 5,5 градусов/минуту.
Совпадение через
90/5,5 ≈ 16 минут