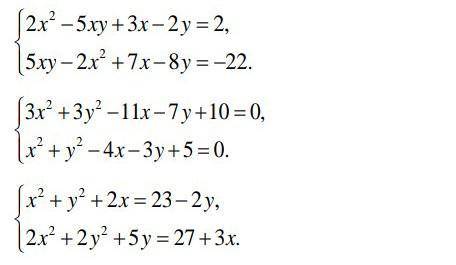
Розв'язання завдання додаю






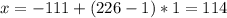
1) Неверно, Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на КОСИНУС угла между ними. Это теорема косинусов.
2) Верно, по теореме Пифагора. 5^2 + 12^2 = 25 + 144 = 169 = 13^2
3) Да, треугольник со сторонами 5, 6, 7 остроугольный, по теореме косинусов.
5^2 + 6^2 = 25 + 36 = 61 > 7^2 = 49
Если сумма квадратов двух меньших сторон больше, чем квадрат наибольшей стороны, то треугольник остроугольный.
Если сумма равна квадрату наибольшей стороны, то прямоугольный.
Если же сумма меньше, чем квадрат наибольшей стороны, то тупоугольный.
4) Да, это верно, это теорема Пифагора.
сложения:
одно из уравнений системы заменим на сумму уравнений:
подстановки: выразим y из второго уравнения и подставляем в первое
D=9-8=1
О т в е т.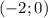 ;
; 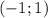
2)
чтобы применить сложения, умножаем второе уравнение на (-3)
сложения:
оставляем второе уравнение, а первое заменяем суммой двух уравнений:
подстановки: выразим x из второго уравнения и подставляем в первое
D=9-8=1
О т в е т. ;
; 
3)
умножаем первое уравнение на (-2)
сложения:
оставляем первое уравнение, а второе заменяем суммой двух уравнений:
подстановки: выразим y из второго уравнения и подставляем в первое
D=25+24=49
О т в е т.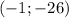 ;
;