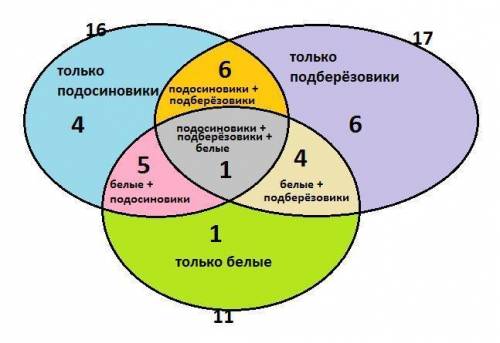
Три вида грибов было в 1 корзине.
Только два вида грибов было :
7 - 1 = 6 корзин - подосиновики и подберёзовики
6 - 1 = 5 корзин - подосиновики и белые
5 - 1 = 4 корзины - подберёзовики и белые
Только один вид грибов был :
16 - 1 - 6 - 5 = 4 корзины - подосиновики
17 - 1 - 6 - 4 = 6 корзин - подберёзовики
11 - 1 - 5 - 4 = 1 корзина - белые
Всего с подосиновиками, подберёзовиками и белыми
1 + 6 + 5 + 4 + 4 + 6 + 1 = 27 корзин.
29 - 27 = 2 корзины были с одними сыроежками.
ответ : 2 гнома принесли одни сыроежки.
Тут разобрано два варианта, когда требуется найти вероятность, что "хотя бы три детали из пяти дефектные" и когда "ровно три детали из пяти дефектные".
Всего у нас изделий 
, изделий имеющих скрытый дефект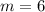 
.
Выбрать 5 изделий из 18 мы можем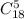 
Выбрать три дефектных, мы можем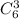 
, остальные 2 можем выбрать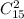 
Вероятность события, равна отношению всех исходов к числу благоприятствующих исходов.
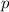(хотя бы 3 из 5 - дефектные детали)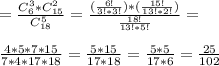 
Если в задаче требуется найти вероятность, когда у нас ровно три дефектных изделия, то меняется только количество какими мы можем вытащить оставшиеся две детали, так как нам теперь не нужно учитывать дефектные. Теперь это будет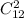 
Соответственно:
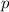(3 из 5 - дефектные детали)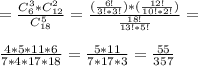 
не розв‘язуючи рівняння x^2+10x-4=0 , знайдіть значення виразу 1/x(1)^2 + 1x(2)^2, де x(1) і x(2) - корені цього рівняння