Объяснение:
Одно число n, следующее за ним (n+1)
Разность квадратов двух последовательных натуральных чисел
(n+1)²-n²
(Из бо`льшего вычитаем меньшее, потому что по условию разности квадратов неотрицательны
Следующие два последовательных натуральных чисел это (n+2) и (n+3)
Разность квадратов следующих двух последовательных натуральных чисел
(n+3)²-(n+2)²
(Здесь тоже из бо`льшего вычитаем меньшее)
Сумма разностей квадратов по условию равна 10
Уравнение
((n+1)²-n²) + ((n+3)²-(n+2)²)=10
(n²+2n+1-n²)+(n²+6n+9-n²-4n-4)=10
2n+1+2n+5=10
4n=4
n=1
1; 2и 3; 4
(2²-1²)+(4²-3²)=10
3+7=10 - верно
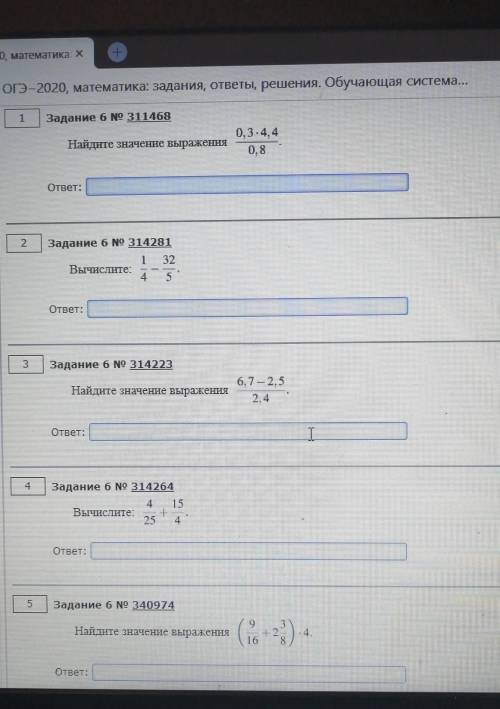
1) 0,3 * 4,4/0,8=0,3 * 44/8=0,3 * 11/2=0,15 * 11=1.5 + 0,15=1,65
это я расписала подробно, как считаю устно.
2) 1/4 - 32/5= 1/4 - 6 2/5=
-(6 8/20 - 5/20)= - 6 3/20
3) (6,7 - 2,5)/2,4=4,2/2,4=42/24=7/4=1 3/4
4) 4/25 + 15/4 = 4/25 + 3 3/4=
3 + 0,16 + 0,75=3,91
5) (9/16 + 2 3/8) * 4=
(9/16 + 19/8) * 4=9*4/16 + 19*4/8=
9/4 + 38/4=47/4 = 11 3/4.