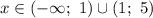Давайте разбираться.
1) Метод сложения. В этом методе подразумевается избавления от одной переменной.
1.1) Рассмотрим простейшую систему:
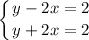
Здесь можно заметить, что если сложить -2х и 2х, то получится 0. Поэтому сложим первое уравнение со вторым и получим:
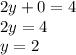
Вот мы нашли одну неизвестную и чтобы найти вторую, надо подставить "у" в любое из двух уравнений, возьмем например первое:
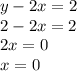
ответ записывается так: (x; y)=(0; 2)
ответ: (0; 2).
1.2) Тут приведу чуть-чуть сложнее систему:
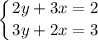
Как видно, если сложить оба уравнения, избавиться от переменной не получится, поэтому надо сделать так, чтобы хоть одна переменная при сложении пропала. Для это мы должны домножить оба уравнения на такие числа, чтобы в результате мы смогли избавиться от переменной. Например мы хотим убрать "у":
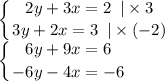
Вот теперь-то видно, что при сложении 6у и -6у получится 0.
Складываем оба уравнения:
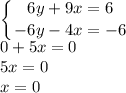
Ну и теперь подставляем "х" в любое уравнение, например в первое:
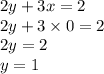
ответ: (0; 1).
2) Метод подстановки. В этом методе мы будем выражать из одного уравнения переменную и подставлять во второе уравнение:
2.1) Рассмотрим систему, в которой не будет дробей:
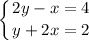
Тут мы выразим "у" из второго уравнения и подставим этот "у" в первое уравнение:
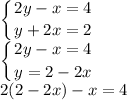
Теперь решаем обычное линейное уравнение:
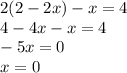
"х" найден и теперь, как в первом методе, подставляем в любое из двух уравнений, например в первое:
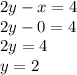
ответ: (0; 2)
2.2) Сложнее система. Тут мы будем работать с дробями:
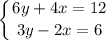
Выразим "x" из второго уравнение и подставим в первое:
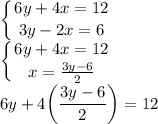
Решаем линейное уравнение:
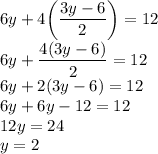
Подставляем "у" в любое уравнение, например во второе:
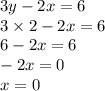
ответ: (0; 2)
Очевидно, это не все случаи, которые могут быть, но это самые распространенные, когда начинают проходить решение систем.
Первый
Анализируем: здесь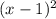 — неотрицательная величина; имеем: при умножении неотрицательной величины с другим выражением мы можем получить отрицательное число, если второе выражение будет отрицательным, а первое — не равным нулю:
— неотрицательная величина; имеем: при умножении неотрицательной величины с другим выражением мы можем получить отрицательное число, если второе выражение будет отрицательным, а первое — не равным нулю:
Итак, общим ответом будет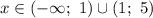
Второй
Решим неравенство методом интервалов:
1) Найдем нули данного выражения:
2) ОДЗ: все числа
3) Начертим координатную прямую и отметим нули данного выражения выколотыми точками (так как неравенство строгое) и определим знак на каждом участке и объединим участок (участки), содержащие знак "минус" (см. вложение).
Итак, общим ответом будет