Объяснение:
Построим функцию.
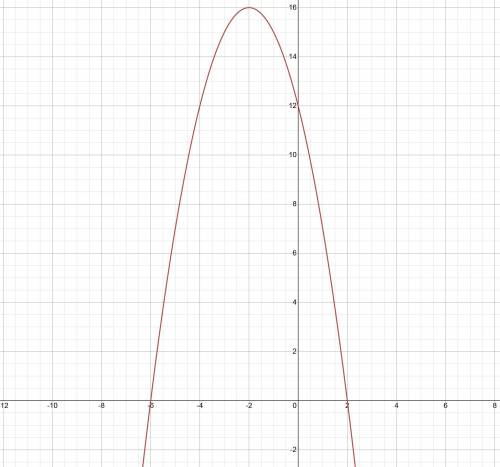
y=(2-х)(х+6)=-x²-4x+12 - парабола ветви направлены вниз
Вершина параболы:
х₀=-(-4)/(-2)=-2
у₀(-2)=-(-2)²+8+12=16
Найдем несколько точек:
х у
2 0
-6 0
0 12
-4 12
Построим параболу.
Опишем свойства функции по графику:
1. Область определения
D(f)=(-∞; +∞)
2. Область значений
E(f)=(-∞; 16]
3. Функция возрастает при x∈(-∞; -2]
функция убывает при х∈[2; +∞)
4. Промежутки знакопостоянства.
Для нашего примера функция положительна при х∈(-6; 2)
Функция отрицательна при х∈(-∞; -6)∪(2; +∞)
5. Нули функции
y(x)=0
x=-6
x=2
6. Четность
График не симетричен относительно оси ОУ - функция нечетная.
7. Точки экстремума, минимума и максимума.
По графику у функции нет точки минимума, есть точка максимума вершина параболы (-2; 16)
Пусть х мер хлеба нужно дать первому человеку.
По условию второй получил на столько больше первого, на сколько третий получит больше второго, четвертый больше третьего, а пятый - больше четвертого.
Обозначим эту разницу как d, тогда
(х+d) мер хлеба нужно дать второму человеку;
(х+d)+d = (х+2d) мер хлеба нужно дать третьему;
(х+2d)+d = (х+3d) мер хлеба нужно дать четвертому;
(х+3d)+d = (х+4d) мер хлеба нужно дать пятому.
1) По условию все вместе получили 100 мер хлеба, получаем уравнение:
х+(х+d)+(х+2d)+(х+3d)+(х+4d)=100
5х+10d=100
Упростив, получаем первое уравнение:
х+2d=20
2) По условию первые два вместе получат в 7 раз меньше трех остальных, получаем уравнение:
7(х+х+d)=х+2d+х+3d+х+4d
Упростим:
14х+7d=3х+9d
11х=2d второе уравнение:
3) Из второго уравнения 2d=11х подставим в первое:
х+11х=20
12х=20
х= ²⁰/₁₂ = ⁵/₃ = 1 ²/₃
Подставим х = ⁵/₃ в уравнение х+2d=20 и найдем d.
⁵/₃+2d=20
2d=20 - ⁵/₃
2d= ⁵⁵/₃
d= ⁵⁵/₆ = 9 ¹/₆
1 ²/₃ мер хлеба первому;
1 ²/₃ + 9 ¹/₆ = 10 ⁵/₆ мер второму;
10 ⁵/₆ + 9 ¹/₆ = 20 мер третьему;
20 + 9 ¹/₆ = 29 ¹/₆ мер четвертому;
29 ¹/₆ + 9 ¹/₆ = 38 ²/₆ = 38 ¹/₃ мер пятому.
ответ. 1 ²/₃; 10 ⁵/⁶; 20; 29 ¹/₆; 38 ¹/₃ .
5ˣ⁺¹ - 3·5ˣ = 250;
5·5ˣ - 3·5ˣ = 250;
2·5ˣ = 250;
5ˣ = 125;
x = 3.
ответ: 3.
4ˣ - 3·2ˣ = 40;
(2ˣ)² - 3·2ˣ - 40 = 0;
замена: 2ˣ = t; t > 0
t² - 3t - 40 = 0;
t₁ = 8; t₂ = -5 - не удовлетворяет условие t > 0.
Обратная замена:
2ˣ = 8
х = 3.
ответ: 3.
log₁₎₈(3x + 4) = log₁₎₈(x² - 4x - 14);
3x + 4 = x² - 4x - 14;
x² - 4x - 14 - 3x - 4 = 0;
x² - 7x - 18 = 0;
x₁ = 9;
x₂ = -2 - не удовлетворяет данное уравнение
ответ: 9.
1 + 2logₓ5 = log₅x|·log₅x;
log₅x + 2 = log²₅x;
log²₅x - log₅x - 2 = 0;
Замена: log₅x = t.
t² - t - 2 = 0;
t₁ = 2;
t₂ = -1.
Обратная замена:
log₅x = 2 или log₅x = -1
x₁ = 25 x₂ = 1/5
ответ: 25; 1/5.