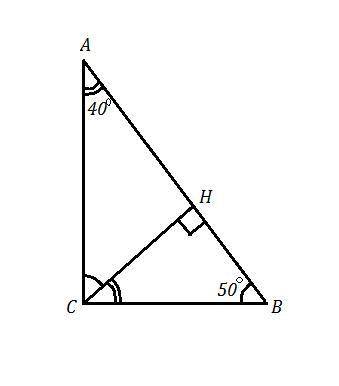
ΔАВС , ∠С=90° , ∠В=50° ⇒ ∠А=90°-∠В=90°-50°=40°
СН ⊥ АВ ⇒ ∠СНА=90° и ∠СРВ=90° .
Рассм. ΔВСН . Он прямоугольный и ∠В=50° , тогда ∠ВСН=90°-50°=40°. Это угол, образованный высотой СН с меньшим катетом (катет ВС лежит против меньшего острого угла ΔАВС).
Рассм. ΔАСН . Он прямоугольный и ∠А=40° , тогда ∠АСН=90°-40°=50°. Это угол, образованный высотой СН с бОльшим катетом АС (катет АС лежит против бОльшего острого угла ΔАВС).
Замечание. Так как у треугольников ΔАВС , ΔВСН и ΔАСН все три угла равны, то эти треугольники подобны .
1) 2,8*(-3,9)=-10,92
76,15:15,23=5
-10,92-5=-15,92
2)7,11+1,56=8,67
34,68:8,67=4
2,45-1,65=0,8
46:0.8=57,5
4+57,5=61,5
3)0,62+0,56-2,29=1,18-2,29=-1,11
8,44-5,34=3,1
-1,11*3,1=3,441