
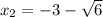
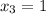

Объяснение:
(x² + 6x)² - 4(x² + 6x + 1) - 17 = 0
t = (x² + 6x)
t² - 4(t + 1) - 17 = 0
t² - 4t - 4 - 17 = 0
t² - 4t - 21 = 0
t² + 3t - 7t - 4 - 17 = 0 (Теорема Виета)
t² + 3t - 7t - 21 = 0
t(t + 3) - 7(t + 3) = 0
(t + 3)(t - 7) = 0
t₁ = -3; t₂ = 7
x² + 6x + 3= 0 x² + 6x - 7 = 0
D = b² - 4ac D = b² - 4ac
D = 6² - 4 * 1 * 3 D = 6² - 4 * 1 * (-7)
D = 36 - 12 D = 36 + 28
D = 24 D = 64
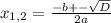



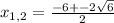

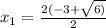

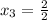
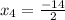

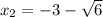
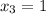

Объяснение:
2х- <4
<4
2x<4+
2x<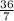 /:2
/:2
х<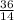
х<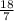
х< 2
х∈(-∞ ; 2 )
)