В шкатулке лежат разноцветные камушки, которые Василий привёз с крымского пляжа. Общее число камушков — 100. Среди них красных — 10, зелёных — 50, прозрачных — 30, синих и чёрных — равное количество. Найди вероятность того, что его брат наугад вытащит синий камень.

👇

Увидеть ответ

Ответ:

апельсинчик19

22.01.2021

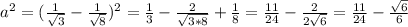
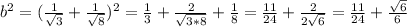
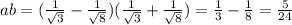
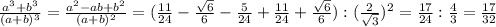
Объяснение:

100-10-50-30=10 камней чёрных и синих вместе

10/2=5 камней синих

Вероятность: 5/100=0,05

4,8(21 оценок)

Открыть все ответы

Ответ:

axeltrofimsky

22.01.2021

несколько недель, и жизнь моя в Белогорской крепости сделалась
для меня не только сносною, но даже и приятно..
2) Жена его им управляла, что согласовалось с его беспечностью.
3) Я стал читать, и во мне пробудилась охота к литературе.
4) Я уже сказывал, что я занимался литературою.
5) Я не вытерпел, вырвал из рук его мою тетрадку и сказал, что уж отроду не покажу ему своих сочинений.
6) А кто эта Маша, перед которой изъясняешься в нежной страсти и в любовной напасти?
7) Обедал почти всегда у коменданта, куда вечерком иногда являлся отец Герасим с женою.
Простые предложения:
1) Я был произведён в офицеры.
2) У Швабрина было несколько французских книг.
3) Мы познакомились.
4) Другого общества в крепости не было.
5) В доме коменданта я был принят как родной.
6) Муж и жена были люди самые почтенные.
7) Марья Ивановна скоро перестала со мною дичиться.
Все предложения взяты из произведения А.С. Пушкина "Капитанская дочка".

4,5(22 оценок)

Ответ:

KINDER123567

22.01.2021

1) $\frac{3}{4-x^2} \geq \frac{1}{4}$
$\frac{3}{4-x^2} - \frac{1}{4} \geq 0$
$\frac{12-(4-x^2)}{4(4-x^2)} \geq 0$
$\frac{8+x^2}{4(2-x)(2+x)} \geq 0$
Числитель и число 4 в знаменателе больше 0 при любом x, поэтому на них можно разделить, все зависит только от скобок в знаменателе:
$\frac{1}{(2-x)(2+x)} \geq 0$
По методу интервалов:
x ∈ (-2; 2)
ответ: D) (-2; 2)

2) $\frac{a^3+b^3}{(a+b)^3} = \frac{(a+b)(a^2-ab+b^2)}{(a+b)^3} =\frac{a^2-ab+b^2}{(a+b)^2}$
Нам дано: $a= \frac{1}{ \sqrt{3} } - \frac{1}{ \sqrt{8} } ; b=\frac{1}{ \sqrt{3} } + \frac{1}{ \sqrt{8} }$
Отсюда: $a+b=\frac{1}{ \sqrt{3} } - \frac{1}{ \sqrt{8} }+\frac{1}{ \sqrt{3} } + \frac{1}{ \sqrt{8} }=\frac{2}{ \sqrt{3} }$
$a^2=(\frac{1}{ \sqrt{3} }-\frac{1}{ \sqrt{8} })^2= \frac{1}{3}- \frac{2}{ \sqrt{3*8} }+ \frac{1}{8}= \frac{11}{24} - \frac{2}{2 \sqrt{6} }= \frac{11}{24} - \frac{ \sqrt{6} }{6}$
$b^2=(\frac{1}{ \sqrt{3} }+\frac{1}{ \sqrt{8} })^2= \frac{1}{3}+ \frac{2}{ \sqrt{3*8} }+ \frac{1}{8}= \frac{11}{24} + \frac{2}{2 \sqrt{6} }= \frac{11}{24} + \frac{ \sqrt{6} }{6}$
$ab=(\frac{1}{ \sqrt{3} }-\frac{1}{ \sqrt{8} })(\frac{1}{ \sqrt{3} }+\frac{1}{ \sqrt{8} })= \frac{1}{3} - \frac{1}{8} = \frac{5}{24}$
Подставляем всё это
$\frac{a^3+b^3}{(a+b)^3} =\frac{a^2-ab+b^2}{(a+b)^2}=(\frac{11}{24} - \frac{ \sqrt{6} }{6}- \frac{5}{24} +\frac{11}{24} + \frac{ \sqrt{6} }{6}):(\frac{2}{ \sqrt{3} })^2= \frac{17}{24} : \frac{4}{3} = \frac{17}{32}$
ответ: A) 17/32

3) |x - 7| - |x + 2| = 9
При x < -2 будет |x - 7| = 7 - x; |x + 2| = -x - 2
7 - x - (-x - 2) = 7 - x + x + 2 = 9
9 = 9 - это истинно для любого x ∈ (-oo; -2)
При -2 <= x < 7 будет |x - 7| = 7 - x; |x + 2| = x + 2
7 - x - (x + 2) = 7 - x - x - 2 = 5 - 2x = 9
-2x = 4; x = -2 - подходит
При x >= 7 будет |x - 7| = x - 7; |x + 2| = x + 2
x - 7 - (x + 2) = x - 7 - x - 2 = 9
-9 = 9
Решений нет
ответ: Е) (-oo; 2]

4,7(94 оценок)

Это интересно:

13.07.2021

Как заново обрести себя и начать жить полноценной жизнью?...

Компьютеры-и-электроника

24.10.2022

Как получить высококачественный звук с помощью Audacity...

Образование-и-коммуникации

14.03.2023

Как провести «зеленое» Рождество?...

Компьютеры-и-электроника

14.05.2023