если пропорция верна, произведение ее крайних членов равно произведению средних членов. поэтому
6,9*5,4=4,6*(2х+5)
2х+5=6,9*5,4/4,6
2х+5=8,1
2х=8,1-5
2х=3,1
х=3,1/2
х=1,55
 натуральное число, тогда
натуральное число, тогда 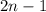 будет натуральным и нечётным числом. Возведем данное число в квадрат:
будет натуральным и нечётным числом. Возведем данное число в квадрат: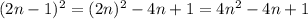

 , 0 делиться на 8, следовательно условие выполняется.
, 0 делиться на 8, следовательно условие выполняется. . Докажем что данное число делиться на 8 при
. Докажем что данное число делиться на 8 при 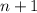 :
:
 делиться на 8. Следовательно, существует натуральный
делиться на 8. Следовательно, существует натуральный 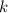 так что:
так что: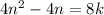
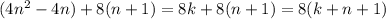 следовательно, при
следовательно, при 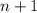 данное число тоже делиться на 8. Ч.Т.Д.
данное число тоже делиться на 8. Ч.Т.Д.
 натуральное число, тогда
натуральное число, тогда 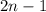 будет натуральным и нечётным числом. Возведем данное число в квадрат:
будет натуральным и нечётным числом. Возведем данное число в квадрат: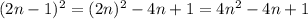

 , 0 делиться на 8, следовательно условие выполняется.
, 0 делиться на 8, следовательно условие выполняется. . Докажем что данное число делиться на 8 при
. Докажем что данное число делиться на 8 при 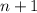 :
:
 делиться на 8. Следовательно, существует натуральный
делиться на 8. Следовательно, существует натуральный 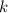 так что:
так что: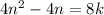
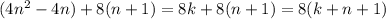 следовательно, при
следовательно, при 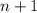 данное число тоже делиться на 8. Ч.Т.Д.
данное число тоже делиться на 8. Ч.Т.Д.
твой пример=(преобразуем дробь и переносим все от х)5дробь23×37,26=2х+5=81дробь10=2х+5=-2х=5-81дробь10=х=1,55
ответ:х=1,55
можешь подставить и проверить.