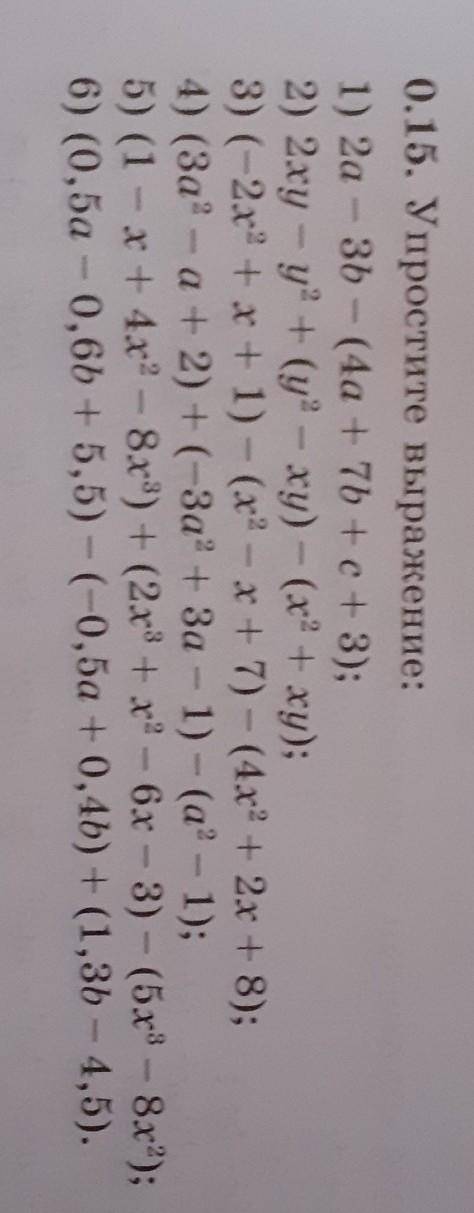
б)a(n)=3n+9
a(1)=12
a(30)=99
S=(a(1)+a(30))/2*n=(12+99)/2*30=1665
Объяснение:
а)существует несколько решения этой задачи. Я предлагаю следующий. Рассмотрю весь набор не пусть чётных двузначных чисел как арифметическую прогрессию. Пусть (a)n - арифметическая прогрессия. Тогда a(1) = 11, a(2) = 13, d = a(2) - a(1) = 2.
Задача тогда сводится к тому. чтобы найти сумму n-первых членов данной арифметической прогрессии.
Всего двузначных нечётных чисел у нас 45. значит надо найти сумму 45 членов этой прогресии.
S(45) =(( 2a(1) + 44d)/2) * 45 =( 2*11+ 88)/2) * 45 = 2475. Вот мы и нашли сумму всех нечётных двузначных чисел.
Раскрываем скобки и приводим подобные слагаемые:
1) 2a-3b-4a-7b-c-3=-2a-10b-c-3;
2) 2xy-y^2+y^2-xy-x^2-xy=(2xy-xy-xy)-(y^2-y^2+y^2)=0-y^2=y^2;
3) -2x^2+x+1-x^2+x-7-4x^2-2x-8= -2x^2-x^2-4x^2+x+x-2x+1-7-8= (-2x^2-x^2-4x^2)+2x-2x+1-15=-7x^2-14=-7(x^2-2);
Объяснение: