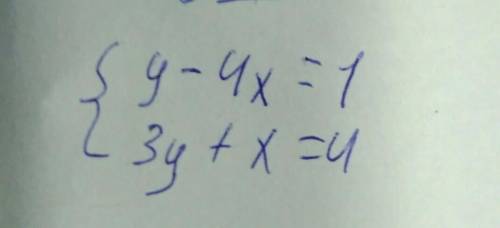
здесь просто нужно выразить температуру (T) из данной формулы...
T^4 = P / (qS), и подставить сюда известные данные:
q = 5.7*10^(-8), S = 1.228*10^20, P = 1.5625*10^25
T^4 = (1.5625*10^25) / (5.7*10^(-8) * 1.228*10^20) = (1.5625 / (5.7 * 1.228)) * 10^13 =
0.22323 * 10^13 = 2.2323 * 10^12
T примерно= 1.2223*10^3 = 1222 (градуса Кельвина)
Если пользоваться калькулятором нельзя, то корень четвертой степени можно извлечь приблизительно...
5.6*1.23 =примерно= 7
1.5625 / 7 = 0.2232
Т^4 =примерно= 0.2232*10^13 = 223*10^10
корень квадратный из 223*10^10 =примерно= 15*10^5
и еще раз корень квадратный из 150*10^4 = 12*10^2 = 1200 (градусов Кельвина)
1) 1+ 1/tg^2(пи/2 +alpha) * sin^2alpha= 1 + 1/ctg^2alpha * sin^2alpha=sin^2alpha*sin^2alpha=sin^4alpha
2) tg^2alpha + sin^2alpha-1/cos^2alpha=tg^2+sin^2alpha-1-tg^2alpha=sin^2alpha-1=-cos^2alplha=cos^2alpha
3)sin^2alpha(1+ctgalpha)+cos^2(1+tg)-sin=sin(1+cos)+cos(1+sin)-sin=sin+2cos*sin+cos-sin=cos(2sin+1)
4) ctg^2alpha - cos^2 alpha- ctg^2 alpha *cos^2 alpha= cos^2/sin^2-cos^2-cos^2/sin^28cos^2alpha=cos^2/sin^2-cos^2-cos^4/sin^2=cos^2-cos^2*sin^2-cos^2/sin^2=cos^2(1-sin^2-cos^2)/sin^2=ctg^2*(cos^2-cos^2)=ctg^2
Відповідь:
Пояснення:
1. Метод підстановки:
2. Метод додавання
3. Графічний метод. Треба побудувати графіки двох прямих
у=4х+1 та у=4/3-1/3 х