Объяснение:
По оси Х есть значения, и по этим значениям выше или ниже или пересекая Ось Х, может находится график. Это "Выше, ниже или пересекая Ось Х- и есть значения "y".
Например: по координатной прямой "х" найдем такую точку, при которой значение графика будет "-1"
Нужно найти точку по Оси "х", в которой по Оси "у" значение будет "-1"Посмотри на график, где по Оси "у"
точка будет "-1" и посчитай по Оси "х" сколько клеток до этой точки нужно пройти?
Это от нуля в право на 6 клеток
запиши это значение для у=-1
х| 6 |
————
у| -1 |
Теперь проверим
Считаем от нуля в право 6 клеточек, и смотрим вниз на 1 клетку. Верно.
Вниз на 1 потому, что "-1"Теперь 0. смотрим по Оси "х" где у=0.
т.е не поднимается и не опускается ни вверх, ни вниз - на нуле. (пересекает Ось Х)
У нас такие три точки: х=0,5; х=5; х≈6,8.
Все эти аргументы верны для значения 0
Далее: у=1;
Имеется 4 точки на графике значение y которых равно 1.
х=0; х=1; х≈4,6; х≈7,2.
И все эти аргументы верны для значения 1
Аналогично ищем остальные точки:
x | 7 | 0,5 | 1 | 8 | -1
———————————>х
y | -1 | 0 | 1 | 3 | 5
Но мы представим 1 как дробь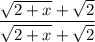 , такое действие еще называют домножением на сопряжённое
, такое действие еще называют домножением на сопряжённое
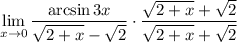
3 Соберем все в одну дробь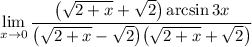
4 Заметим в знаменателе разность квадратов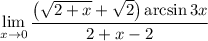
5 Упростим знаменатель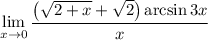
6 Представим дробь как произведениеНо 1 мы представим в виде
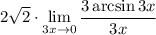
11 Вынесем константу (3) за предел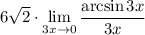
12 Имеем первый замечательный предел, он равен 1