task/29410264 Упростите выражения
а) (p-2a)(p+2a)-(p-a)(p²+pa+a² )
б) 3•(2a- 5b)² - 12(a-b)²
а) (p-2a)(p+2a)-(p-a)(p²+pa+a² ) =p²-(2a)² -(p³ - a³) = p²- 4a² - p³ + a³ .
б) 3•(2a- 5b)² - 12(a-b)² =3(4a² -20ab +25b²) - 12(a²-2ab+b²) = 12a² - 60ab +75b² - 12a² +24ab - 12b² = 63b² - 36ab .
или
3•(2a- 5b)² - 12(a-b)² =3•( (2a- 5b)² - 4*(a-b)² ) = 3•( (2a- 5b)² - (2a-2b)² ) = 3(2a - 5b - 2a +2b)(2a- 5b+2a-2b ) = -9b(4a- 7b ) = 63b² - 36ab .
Все стороны квадрата равны. Допустим сторона квадра будет x.
Тогда площадь квадрата будет равна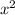
. По условию площадь увеличилась в 16 раз, то есть стала равна 
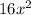. Так как она увеличилась, следовательно увеличили саму сторону квадрата. Увеличили ее в 4 раза, так как новая площадь это 
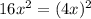. Мы узнали, что сторона квадрата увеличилась в 4 раза, теперь узнаем во сколько раз увеличится периметр. Так как периметр квадрата без увеличение его сторон будет равен 4x, то при увеличении стороны в 4 раза он будет равен 4*4x=16x. То есть периметр увеличился в 4 раза.